
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
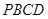 ,
,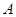 为
为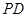 上一点,且
上一点,且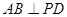 ,
,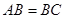 ,
,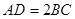 ,沿着
,沿着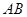 折叠使得二面角
折叠使得二面角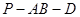 为
为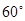 的二面角,连结
的二面角,连结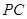 、
、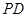 ,在
,在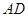 上取一点
上取一点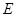 使得
使得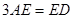 ,连结
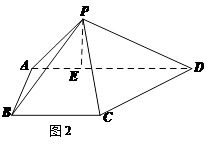
,连结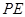 得到如下图(图2)的一个几何体.
得到如下图(图2)的一个几何体.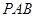
 平面
平面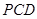 ;
;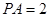 ,求点
,求点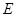 到平面
到平面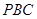 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
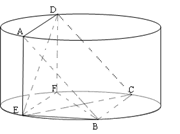
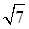 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过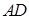 作圆柱的截面交下底面于
作圆柱的截面交下底面于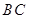 .
.
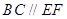 ;
;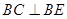 ;
;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
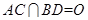 ,
,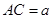 ,得到三棱锥
,得到三棱锥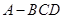 ,如图所示。
,如图所示。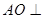 平面BCD;
平面BCD;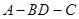 的大小为
的大小为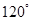 时,
时,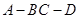 的正切值。
的正切值。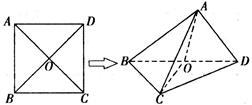
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
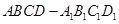 是正方体,点
是正方体,点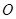 为正方体对角线的交点,过点
为正方体对角线的交点,过点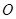 的任一平面
的任一平面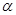 ,正方体的八个顶点到平面
,正方体的八个顶点到平面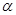 的距离作为集合
的距离作为集合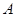 的元素,则集合
的元素,则集合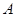 中的元素个数最多为_____ ___个.
中的元素个数最多为_____ ___个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com