[题目]如图.在矩形ABCD中.AB=1.AD= .P矩形内的一点.且AP= .若 ..則λ+ μ的最大值为．题目和参考答案——青夏教育精英家教网—

【题目】如图，在矩形ABCD中，AB=1，AD= ，P矩形内的一点，且AP= ，若，（λ，μ∈R），則λ+ μ的最大值为．

【答案】
【解析】解：如图所示，在图中，设P（x，y）．
B（1，0），D（0，），C（1，），
由AP= ，x2+y2= ，
则点P满足的约束条件为，
∵ ，
即（x，y）=λ（1，0）+μ（0，），
∴x=λ，y= μ，
∴λ+ =x+y，
由于x+y≤ = = 当且仅当x=y时取等号．
则λ+ =x+y的最大值为，
所以答案是：

【考点精析】通过灵活运用平面向量的基本定理及其意义，掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使即可以解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】数列{an}与{bn}满足：①a1=a＜0，b1=b＞0，②当k≥2时，若ak﹣1+bk﹣1≥0，则ak=ak﹣1 ， bk= ；若ak﹣1+bk﹣1＜0，则ak= ，bk=bk﹣1 ．
（Ⅰ）若a=﹣1，b=1，求a2 ， b2 ， a3 ， b3的值；
（Ⅱ）设Sn=（b1﹣a1）+（b2﹣a2）+…+（bn﹣an），求Sn（用a，b表示）；
（Ⅲ）若存在n∈N* ，对任意正整数k，当2≤k≤n时，恒有bk﹣1＞bk ，求n的最大值（用a，b表示）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f(x)＝(x－a)(x－b)(其中a＞b)，若f(x)的图象如图所示，则函数g(x)＝ax＋b的图象大致为(　　)

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择．为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏．
（Ⅰ）求这4个人中恰有2人去参加甲游戏的概率；
（Ⅱ）用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记ξ=|X﹣Y|，求随机变量ξ的分布列与数学期望Eξ．

查看答案和解析>>

科目：高中数学 来源： 题型：

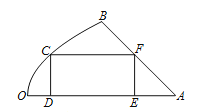
【题目】如图是一块地皮，其中，是直线段，曲线段是抛物线的一部分，且点是该抛物线的顶点，所在的直线是该抛物线的对称轴．经测量， km， km，．现要从这块地皮中划一个矩形来建造草坪，其中点在曲线段上，点，在直线段上，点在直线段上，设km，矩形草坪的面积为km2．