【题目】已知函数
（
， 
）为奇函数，且相邻两对称轴间的距离为
.
（1）当
时，求
的单调递减区间；
（2）将函数
的图象沿
轴方向向右平移
个单位长度，再把横坐标缩短到原来的
（纵坐标不变），得到函数
的图象.当
时，求函数
的值域.
快捷英语周周练系列答案科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝|2x－1|＋|x－2a|.
(1)当a＝1时，求f(x)≤3的解集；
(2)当x∈[1，2]时，f(x)≤3恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】通过研究学生的学习行为，心理学家发现，学生接受能力依赖于老师引入概念和描述问题所用的时间，讲座开始时，学生的兴趣激增，中间有一段不太长的时间，学生的兴趣保持理想的状态，随后学生的注意力开始分散，分析结果和实验表明，用
表示学生掌握和接受概念的能力（
的值越大，表示接受能力越强），
表示提出和讲授概念的时间（单位：分），可以有以下公式：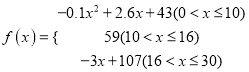 
．
（1）开讲多少分钟后，学生的接受能力最强？能维持多少分钟？
（2）开讲5分钟与开讲20分钟比较，学生的接受能力何时强一些？
（3）一个数学难题，需要55的接受能力以及13分钟的时间，老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题：①集合
的子集个数有16个；②定义在
上的奇函数
必满足
；③
既不是奇函数又不是偶函数；④偶函数的图像一定与
轴相交；⑤
在
上是减函数。
其中真命题的序号是 ______________（把你认为正确的命题的序号都填上）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于函数①f（x）=4x+
-5，②f（x）=|log2 x|-（
）x，③f（x）=cos（x+2）-cosx，判断如下两个命题的真假：
命题甲：f（x）在区间（1，2）上是增函数；
命题乙：f（x）在区间（0，+∞）上恰有两个零点x1，x2，且x1x2<1.
能使命题甲、乙均为真的函数的序号是_____________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等差数列{an}的前3项和为6，前8项和为－4.
(1)求数列{an}的通项公式；
(2)设bn＝(4－an)qn－1 (q≠0，n∈N*)，求数列{bn}的前n项和Sn.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线y2＝2px(p>0)的焦点为F，A是抛物线上横坐标为4，且位于x轴上方的点，A到抛物线准线的距离等于5，过A作AB垂直于y轴，垂足为B，OB的中点为M.
(1)求抛物线的方程；
(2)以M为圆心，MB为半径作圆M，当K(m,0)是x轴上一动点时，讨论直线AK与圆M的位置关系．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列命题：
①若(1－x)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5，则|a1|＋|a2|＋|a3|＋|a4|＋|a5|＝32
②α，β，γ是三个不同的平面，则“γ⊥α，γ⊥β”是“α∥β”的充分条件
③已知sin
＝
，则cos
＝
.其中正确命题的个数为( )
A．0 B．1
C．2 D．3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
）在
上的最小值为
，当把
的图象上所有的点向右平移
个单位后，得到函数
的图象．
（1）求函数
的解析式；
（2）在△
中，角
，
，
对应的边分别是
，
，
，若函数
在
轴右侧的第一个零点恰为
，
，求△
的面积
的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
