
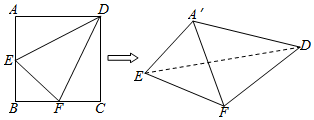
分析 (1)根据A′D,A′E,A′F两两垂直可得A′E⊥平面A′DF,故而V棱锥A′-EFD=V棱锥E-A′DF=$\frac{1}{3}{S}_{△A′DF}•A′E$;
(2)过A′作A′O⊥平面DEF,连结DO,则∠A′DO为直线A′D与平面DEF所成的角,利用等体积法求出A′O,即可得出∠A′DO的正弦值.
解答 解:(1)∵A′E⊥A′D,A′E⊥A′F,A′D?平面A′DF,A′F?平面A′DF,
∴A′E⊥平面A′DF,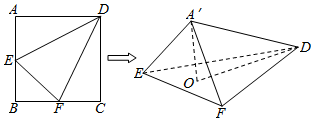
∵A′E=1,A′D=2,A′F=1,
∴V棱锥A′-EFD=V棱锥E-A′DF=$\frac{1}{3}{S}_{△A′DF}•A′E$=$\frac{1}{3}×\frac{1}{2}×1×2×1$=$\frac{1}{3}$.
(2)过A′作A′O⊥平面DEF,连结DO,则∠A′DO为直线A′D与平面DEF所成的角.
∵S△DEF=S正方形ABCD-S△ADE-S△BEF-S△CDF=2×2-$\frac{1}{2}×1×2$-$\frac{1}{2}×1×1$-$\frac{1}{2}×1×2$=$\frac{3}{2}$,
∴V棱锥A′-DEF=$\frac{1}{3}{S}_{△DEF}•A′O$=$\frac{1}{2}$A′O=$\frac{1}{3}$,
∴A′O=$\frac{2}{3}$,
∴sin∠A′DO=$\frac{A′O}{A′D}$=$\frac{1}{3}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,线面角的计算,属于中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | $\frac{b}{a}>1$ | C. | a2<b2 | D. | ab<a+b-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
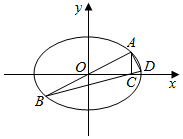 直线y=kx(k>0)与E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1交于A,B,C在x轴上,且AC⊥x轴,直线BC与E交于D,若AB⊥AD,则E的离心率为( )
直线y=kx(k>0)与E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1交于A,B,C在x轴上,且AC⊥x轴,直线BC与E交于D,若AB⊥AD,则E的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45% | B. | 25% | C. | 9% | D. | 65% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com