
分析 判断几何体体积最大时的结构特征,然后利用四面体的结构特征,求解球的半径.
解答 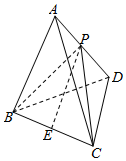 解:△ABC和△BCD都是边长为4的正三角形三棱锥的体积的最大值,是A到底面的距离最大时取得,就是侧面ABC与底面BCD垂直时取得最大值,
解:△ABC和△BCD都是边长为4的正三角形三棱锥的体积的最大值,是A到底面的距离最大时取得,就是侧面ABC与底面BCD垂直时取得最大值,
此时△ABD和△ACD是全等的等腰三角形,其腰长为4,底边长为x,
∵设E,P为BC,AD的中点,
∴可以判断三角形AED为等腰直角三角形,
∴AE=$2\sqrt{3}$,BE=2,
AD=$\sqrt{2}AE$=2$\sqrt{6}$,PE=$\frac{1}{2}$AD=$\sqrt{6}$,
∵根据几何体的结构特征得出外接球的球心O在EP上,
∴设OE=h,
OP=$\sqrt{6}$-h,
∴$\left\{\begin{array}{l}{{R}^{2}={2}^{2}+{h}^{2}}\\{{R}^{2}=(\sqrt{6}-h)^{2}+(\sqrt{6})^{2}}\end{array}\right.$,
即h=$\frac{4}{\sqrt{6}}$,R2=$\frac{20}{3}$,
其外接球的表面积为:4πR2=$\frac{80π}{3}$,
故答案为:$\frac{80π}{3}$.
点评 本题考查了空间几何体体积和表面积,考查了学生的空间想象能力和数学转化能力,此题是中档题


科目:高中数学 来源: 题型:解答题
| 销售量x(吨) | 2 | 3 | 5 | 6 |
| 销售收入y(千元) | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
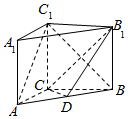 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5海里 | B. | $5\sqrt{3}$海里 | C. | 10海里 | D. | $10\sqrt{3}$海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0)点 | B. | ($\overline{x}$,$\overline{y}$)点 | C. | (0,$\overline{y}$)点 | D. | ($\overline{x}$,0)点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com