
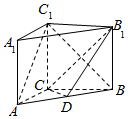
 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.分析 (1)以C为坐标原点,以CA,CB,CC1为坐标轴建立空间直角坐标系,求出$\overrightarrow{AC}$和$\overrightarrow{B{C}_{1}}$的坐标,通过计算$\overrightarrow{AC}•\overrightarrow{B{C}_{1}}$=0得出AC⊥BC1;
(2)设BC1与CB1的交点为O,求出$\overrightarrow{DO}$的坐标,通过证明$\overrightarrow{A{C}_{1}}∥\overrightarrow{DO}$得出AC1∥DO得出AC1∥平面CDB1;
(3)过D作DE⊥BC,连结B1E,则DE⊥平面BCC1B1,于是∠DB1E为直线DB1与平面BCC1B1所成的角.利用勾股定理求出DE,B1E,计算tan∠DB1E.
解答 解:∵AC=3,BC=4,AB=5,∴AC2+BC2=AB2,∴AC⊥BC.
以C为坐标原点,以CA,CB,CC1为坐标轴建立空间直角坐标系,如图所示:
(1)A(3,0,0),C(0,0,0),B(0,4,0),C1(0,0,4),
∴$\overrightarrow{AC}$=(-3,0,0),$\overrightarrow{B{C}_{1}}$=(0,-4,4),
∴$\overrightarrow{AC}•\overrightarrow{B{C}_{1}}$=0,
∴AC⊥BC1
(2)设BC1与CB1的交点为O,则O为BC1的中点,∴O(0,2,2),
∵D是AB的中点,∴D($\frac{3}{2}$,2,0),
∴$\overrightarrow{DO}$=(-$\frac{3}{2}$,0,2),$\overrightarrow{A{C}_{1}}$=(-3,0,4),
∴$\overrightarrow{A{C}_{1}}$=2$\overrightarrow{DO}$,
∴AC1∥DO,又DO?平面B1CD,AC1?平面B1CD,
∴AC1∥平面CDB1.
(3)过D作DE⊥BC,连结B1E,则DE⊥平面BCC1B1,
∴∠DB1E为直线DB1与平面BCC1B1所成的角.
∵D是AB的中点,∴DE=$\frac{1}{2}AC$=$\frac{3}{2}$,BE=$\frac{1}{2}BC=2$,
∴B1E=$\sqrt{B{E}^{2}+B{{B}_{1}}^{2}}$=2$\sqrt{5}$.
∴tan∠DB1E=$\frac{DE}{{B}_{1}E}$=$\frac{3\sqrt{5}}{20}$.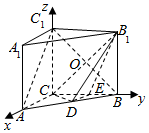
点评 本题考查了线面平行,直线垂直的判定,线面角的计算,属于中档题.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$π | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
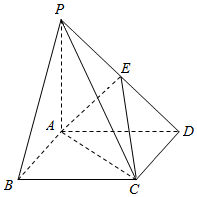 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
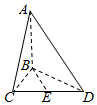 如图,四面体ABCD中,AB,BC,CD,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为$\frac{\sqrt{10}}{10}$,则直线BE与平面ACD所成角的正弦值为( )
如图,四面体ABCD中,AB,BC,CD,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为$\frac{\sqrt{10}}{10}$,则直线BE与平面ACD所成角的正弦值为( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
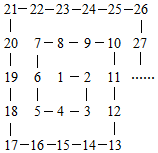 将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )
将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )| A. | 1006010 | B. | 1006110 | C. | 1017073 | D. | 1017072 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,气象部门预报,在海面上生成了一股较强台风,在据台风中心60千米的圆形区域内将受到严重破坏,台风中心这个从海岸M点登陆,并以72千米/小时的速度沿北偏西60°的方向移动,已知M点位于A城的南偏东15°方向,距A城$61\sqrt{2}$千米;M点位于B城的正东方向,距B城$60\sqrt{3}$千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题:
如图,气象部门预报,在海面上生成了一股较强台风,在据台风中心60千米的圆形区域内将受到严重破坏,台风中心这个从海岸M点登陆,并以72千米/小时的速度沿北偏西60°的方向移动,已知M点位于A城的南偏东15°方向,距A城$61\sqrt{2}$千米;M点位于B城的正东方向,距B城$60\sqrt{3}$千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com