
| A. | $\frac{3}{4}$π | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
分析 作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案
解答  解:作函数f(x)的图象(如图)
解:作函数f(x)的图象(如图)
观察图象,得:若f(x)=a有解,则a∈[0,1]
①$\frac{\sqrt{2}}{2}$<a<1,f(x)=a有4解,S=π,
②a=$\frac{\sqrt{2}}{2}$,f(x)=a有三解,S=$\frac{3}{4}π$,
③0<a<$\frac{\sqrt{2}}{2}$或a=1,f(x)=a有2解,S=$\frac{π}{2}$.
∴S不可能为2π.
故选:D.
点评 本题考查图象变换法求函数解析式的方法,考查根的存在性及根的个数的判断,其中根据函数y=f(x)的图象关于直线x=$\frac{π}{4}$对称,当x≥$\frac{π}{4}$时,f(x)=sinx,根据对称变换法则,作出函数的图象是解答本题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
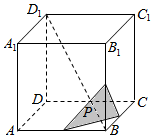 如图,在正方体ABCD-A1B1C1D1中,AB=1,点P为BD1上一点,平面α满足:点P∈平面α,直BD1⊥平面α,设以B为顶点,以连接平面α与正方体棱的交点为底面的几何体的体积为V,则V的最大值为( )
如图,在正方体ABCD-A1B1C1D1中,AB=1,点P为BD1上一点,平面α满足:点P∈平面α,直BD1⊥平面α,设以B为顶点,以连接平面α与正方体棱的交点为底面的几何体的体积为V,则V的最大值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{16}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 是非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某村欲修建一横断面为等腰梯形的水渠(如图),为降低成本,必须尽量减少水与水渠壁的接触面,若水渠的横断面面积设计为定值m,渠深3米,则水渠侧壁的倾斜角α应为多少时,方能使修建成本最低?
某村欲修建一横断面为等腰梯形的水渠(如图),为降低成本,必须尽量减少水与水渠壁的接触面,若水渠的横断面面积设计为定值m,渠深3米,则水渠侧壁的倾斜角α应为多少时,方能使修建成本最低?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
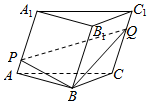 如图,设三棱柱ABC-A1B1C1的体积为2,P、Q分别是侧棱AA1、CC1上的点,且AP=QC1,则四棱锥B-APQC的体积为$\frac{2}{3}$.
如图,设三棱柱ABC-A1B1C1的体积为2,P、Q分别是侧棱AA1、CC1上的点,且AP=QC1,则四棱锥B-APQC的体积为$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
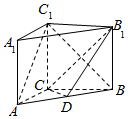 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com