
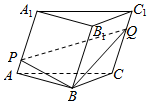
 如图,设三棱柱ABC-A1B1C1的体积为2,P、Q分别是侧棱AA1、CC1上的点,且AP=QC1,则四棱锥B-APQC的体积为$\frac{2}{3}$.
如图,设三棱柱ABC-A1B1C1的体积为2,P、Q分别是侧棱AA1、CC1上的点,且AP=QC1,则四棱锥B-APQC的体积为$\frac{2}{3}$. 分析 由已知中三P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,我们可得SAPQC=$\frac{1}{2}$${S}_{AC{C}_{1}{A}_{1}}$,即VB-APQC=$\frac{1}{2}{V}_{B-AC{C}_{1}{A}_{1}}$,再结合同底等高的棱柱的体积为棱锥体积的3倍,即可求出答案.
解答 解:∵P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,
∴四棱锥B-APQC的底面积SAPQC=$\frac{1}{2}$${S}_{AC{C}_{1}{A}_{1}}$
∵VB-ACC1A1=${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$-${V}_{B-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{4}{3}$
∴VB-APQC=$\frac{1}{2}{V}_{B-AC{C}_{1}{A}_{1}}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查的知识点是棱柱的体积、棱锥的体积,其中分析出棱锥与原棱柱之间底面积、高之间的比例关系是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$π | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
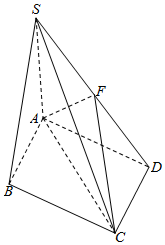 如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
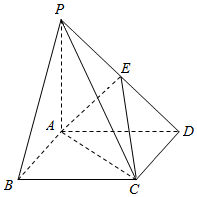 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
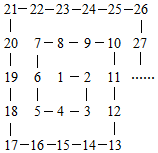 将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )
将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )| A. | 1006010 | B. | 1006110 | C. | 1017073 | D. | 1017072 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com