
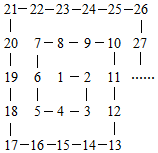 将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )
将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )| A. | 1006010 | B. | 1006110 | C. | 1017073 | D. | 1017072 |
分析 观察由1起每一个转弯时递增的数字可发现为“1,1,2,2,3,3,4,4,…”.由此能求出在第2016个转弯处的数.
解答 :观察由1起每一个转弯时递增的数字,
可发现为“1,1,2,2,3,3,4,4,…”,
即第一、二个转弯时递增的数字都是1,
第三、四个转弯时递增的数字都是2,
第五、六个转弯时递增的数字都是3,
第七、八个转弯时递增的数字都是4,
…
故在第2016个转弯处的数为:
1+2(1+2+3+…+1008)
=1+2×$\frac{1008(1+1008)}{2}$
=1017073.
故选:C
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源: 题型:填空题
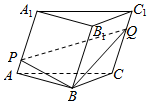 如图,设三棱柱ABC-A1B1C1的体积为2,P、Q分别是侧棱AA1、CC1上的点,且AP=QC1,则四棱锥B-APQC的体积为$\frac{2}{3}$.
如图,设三棱柱ABC-A1B1C1的体积为2,P、Q分别是侧棱AA1、CC1上的点,且AP=QC1,则四棱锥B-APQC的体积为$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
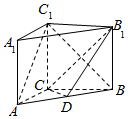 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5海里 | B. | $5\sqrt{3}$海里 | C. | 10海里 | D. | $10\sqrt{3}$海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
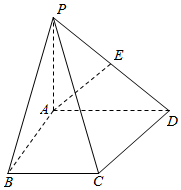 如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.
如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0)点 | B. | ($\overline{x}$,$\overline{y}$)点 | C. | (0,$\overline{y}$)点 | D. | ($\overline{x}$,0)点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com