
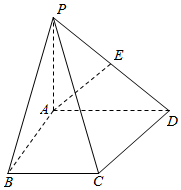
 如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.
如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.分析 (1)以A为坐标原点建立空间直角坐标系,求出各点坐标得出$\overrightarrow{BE}$和$\overrightarrow{PD}$的坐标,通过计算$\overrightarrow{BE}•\overrightarrow{PD}$=0得出BE⊥PD;
(2)由(1)可知$\overrightarrow{PD}$为平面ABE的一个法向量,求出$\overrightarrow{PC},\overrightarrow{PD}$的夹角<$\overrightarrow{PC}$,$\overrightarrow{PD}$>,则直线PC与平面ABE所成角为$\frac{π}{2}$-<$\overrightarrow{PC}$,$\overrightarrow{PD}$>.
解答 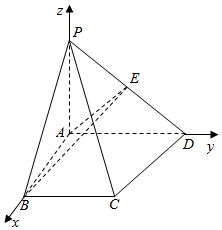 解:(1)∵PA⊥平面ABCD,
解:(1)∵PA⊥平面ABCD,
∴∠PDA为PD与底面ABCD所成的角,即∠PDA=30°,
∴PA=$\frac{\sqrt{3}}{3}$AD=$\frac{2\sqrt{3}a}{3}$,AE=a,∠DAE=60°,
以A为坐标原点建立空间直角坐标系A-xyz如图所示:
则A(0,0,0),B(a,0,0),C(a,a,0),D(0,2a,0),E(0,$\frac{a}{2}$,$\frac{\sqrt{3}a}{2}$),P(0,0,$\frac{2\sqrt{3}a}{3}$).
∴$\overrightarrow{BE}$=(-a,$\frac{a}{2}$,$\frac{\sqrt{3}a}{2}$),$\overrightarrow{PD}$=(0,2a,-$\frac{2\sqrt{3}a}{3}$).
∴$\overrightarrow{BE}•\overrightarrow{PD}$=-a×0+$\frac{a}{2}$×2a+$\frac{\sqrt{3}a}{2}$×(-$\frac{2\sqrt{3}a}{3}$)=0.
∴BE⊥PD.
(2)∵PD⊥BE,PD⊥AE,AE?平面ABE,BE?平面ABE,AE∩BE=E,
∴PD⊥平面ABE,∴$\overrightarrow{PD}$为平面ABE的一个法向量.
∵$\overrightarrow{PC}$=(a,a,-$\frac{2\sqrt{3}a}{3}$),∴$\overrightarrow{PC}•\overrightarrow{PD}$=$\frac{10{a}^{2}}{3}$,|$\overrightarrow{PC}$|=$\frac{\sqrt{30}a}{3}$,|$\overrightarrow{PD}$|=$\frac{4\sqrt{3}a}{3}$,
∴cos<$\overrightarrow{PC}$,$\overrightarrow{PD}$>=$\frac{\overrightarrow{PC}•\overrightarrow{PD}}{|\overrightarrow{PC}||\overrightarrow{PD}|}$=$\frac{\sqrt{10}}{4}$,
∴直线PC与平面ABE所成角的正弦值为$\frac{\sqrt{10}}{4}$,
∴直线PC与平面ABE所成角的余弦值为$\sqrt{1-(\frac{\sqrt{10}}{4})^{2}}$=$\frac{\sqrt{6}}{4}$.
点评 本题考查了空间向量在立体几何中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
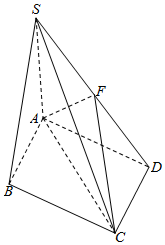 如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
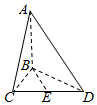 如图,四面体ABCD中,AB,BC,CD,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为$\frac{\sqrt{10}}{10}$,则直线BE与平面ACD所成角的正弦值为( )
如图,四面体ABCD中,AB,BC,CD,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为$\frac{\sqrt{10}}{10}$,则直线BE与平面ACD所成角的正弦值为( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
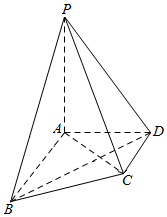 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,PA=AB=2CD=4,$PB=2AD=4\sqrt{2}$,平面PAB⊥平面ABCD.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,PA=AB=2CD=4,$PB=2AD=4\sqrt{2}$,平面PAB⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
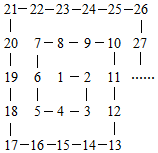 将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )
将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )| A. | 1006010 | B. | 1006110 | C. | 1017073 | D. | 1017072 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
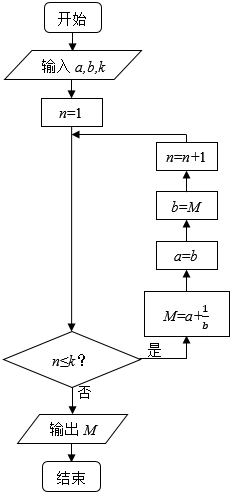 执行如图的程序框图,若输入a,b,k分别为1,2,3,则输出的M=( )
执行如图的程序框图,若输入a,b,k分别为1,2,3,则输出的M=( )| A. | $\frac{2}{3}$ | B. | $\frac{16}{5}$ | C. | $\frac{7}{2}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{3},\frac{2}{3}]$ | B. | $[\frac{1}{6},\frac{4}{3}]$ | C. | $[\frac{1}{3},\frac{4}{3}]$ | D. | $[\frac{2}{3},\frac{4}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 认为作业多 | 认为作业不多 | 总计 | |
| 喜欢玩电脑游戏 | 18 | 12 | 30 |
| 不喜欢玩电脑游戏 | 5 | 16 | 21 |
| 总计 | 23 | 28 | 51 |
| A. | 有95%的把握认为喜欢玩电脑游戏与认为作业多少有关 | |
| B. | 有95%的把握认为喜欢玩电脑游戏与认为作业多少无关 | |
| C. | 有99%的把握认为喜欢玩电脑游戏与认为作业多少有关 | |
| D. | 有99%的把握认为喜欢玩电脑游戏与认为作业多少无关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com