
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)计算K2,对照附表做结论;
(2)作出甲,乙两人解答时间的平面区域,找出乙比甲早做完对于的区域,则区域面积的比值即为所求概率;
(3)使用组合数公式和古典概型的概率计算公式分别计算X取不同值时的概率,得到X的分布列,求出数学期望.
解答 解:(1)由表中数据得K2的观测值K2=$\frac{50(22×12-8×8)^{2}}{30×20×30×20}$=$\frac{50}{9}≈5.556$>5.024.
所以根据统计有97.5%的把握认为视觉和空间能力与性别有关.
(2)设甲、乙解答一道几何题的时间分别为x,y分钟,
则基本事件满足的区域为$\left\{\begin{array}{l}{5≤x≤7}\\{6≤y≤8}\end{array}\right.$(如图所示).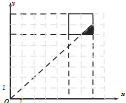
设事件A为“乙比甲先做完此道题”
则满足的区域为x>y.
∴P(A)=$\frac{\frac{1}{2}×1×1}{2×2}$=$\frac{1}{8}$
即乙比甲先解答完的概率为$\frac{1}{8}$.
(3)在选择做几何题的8名女生中任意抽取两人,抽取方法有${C}_{8}^{2}$=28 种,
其中甲、乙两人都不被被抽到有${C}_{6}^{2}$=15种;恰有一人被抽到有${C}_{2}^{1}$•${C}_{6}^{1}$=12种;两人都被抽到有${C}_{2}^{2}$=1种.
X可能取值为0,1,2,
P(X=0)=$\frac{15}{28}$,P(X=1)=$\frac{12}{28}=\frac{3}{7}$,P(X=2)=$\frac{1}{28}$.
X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{15}{28}$ | $\frac{3}{7}$ | $\frac{1}{28}$ |
点评 本题考查了独立性检验的统计思想,几何概型的概率计算,离散性随机变量的分布列和数学期望.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
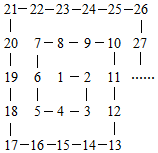 将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )
将正整数1,2,3,4…排列成阵(如图),在2处转第一个弯,在3处转第二个弯,在5处转第三个弯,…则第2016个转弯处的数为( )| A. | 1006010 | B. | 1006110 | C. | 1017073 | D. | 1017072 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,气象部门预报,在海面上生成了一股较强台风,在据台风中心60千米的圆形区域内将受到严重破坏,台风中心这个从海岸M点登陆,并以72千米/小时的速度沿北偏西60°的方向移动,已知M点位于A城的南偏东15°方向,距A城$61\sqrt{2}$千米;M点位于B城的正东方向,距B城$60\sqrt{3}$千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题:
如图,气象部门预报,在海面上生成了一股较强台风,在据台风中心60千米的圆形区域内将受到严重破坏,台风中心这个从海岸M点登陆,并以72千米/小时的速度沿北偏西60°的方向移动,已知M点位于A城的南偏东15°方向,距A城$61\sqrt{2}$千米;M点位于B城的正东方向,距B城$60\sqrt{3}$千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 15 | 25 | 50 | 70 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 认为作业多 | 认为作业不多 | 总计 | |
| 喜欢玩电脑游戏 | 18 | 12 | 30 |
| 不喜欢玩电脑游戏 | 5 | 16 | 21 |
| 总计 | 23 | 28 | 51 |
| A. | 有95%的把握认为喜欢玩电脑游戏与认为作业多少有关 | |
| B. | 有95%的把握认为喜欢玩电脑游戏与认为作业多少无关 | |
| C. | 有99%的把握认为喜欢玩电脑游戏与认为作业多少有关 | |
| D. | 有99%的把握认为喜欢玩电脑游戏与认为作业多少无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=10$\sqrt{3}$km,则OA2+OB2=200.
如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=10$\sqrt{3}$km,则OA2+OB2=200.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 152种 | B. | 54种 | C. | 90种 | D. | 126种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com