练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．我国的邮政编码由六位数字组成，最后两位数字是一个邮政局的投递区编号，代表一个镇或者一个居住的小区，那么，一个投递区最多有多少个编号呢？

    分析 利用计数原理，求解即可．

    解答 解：我国的邮政编码由六位数字组成，最后两位数字是一个邮政局的投递区编号，
    代表一个镇或者一个居住的小区，一个投递区的两位数数值可以相同，也可以不相同，所以个位数有10种方法，十位数数值也有10种方法，
    共有100种编号．
    故答案为：100．

    点评 本题考查计数原理的应用，考查分析问题解决问题的能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0），以C的右焦点F（c，0）为圆心，以a为半径的圆与C的一条渐近线交于A，B两点，若|AB|=$\frac{2}{3}$c，则双曲线C的离心率为（　　）
    A．$\frac{{3\sqrt{26}}}{13}$B．$\frac{{3\sqrt{5}}}{5}$C．$\frac{{\sqrt{6}}}{2}$D．$\frac{3}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

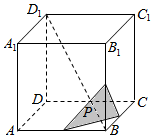    7．如图，在正方体ABCD-A1B1C1D1中，AB=1，点P为BD1上一点，平面α满足：点P∈平面α，直BD1⊥平面α，设以B为顶点，以连接平面α与正方体棱的交点为底面的几何体的体积为V，则V的最大值为（　　）
    A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{3}{16}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．如图，已四棱锥P-ABCD的底面是正方形，PA⊥底面ABCD，且PA=AD=2，点M、N分别在PD、PC上，2PN=NC，PM=MD
    （1）求证：PC⊥平面AMN；
    （2）求四面体P-ABN的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

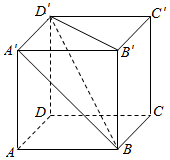    11．如图所示，在棱长为2的正方体ABCD-A′B′C′D′中，求：
    （1）二面角B-A′D′-D的平面角的正切值；
    （2）三棱锥A′-BB′D′的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．8个人排成一排，若要求甲、乙、丙三人必须站在一起，则不同的排法有（　　）
    A．${A}_{8}^{8}$种B．3${A}_{7}^{7}$种C．3${A}_{6}^{6}$种D．${A}_{3}^{3}$${A}_{6}^{6}$种

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知函数F（x）=$\frac{{3}^{x}cos4x}{{9}^{x}-1}$f（x）（x≠0）是偶函数，且f（x）不恒等于零，则f（x）（　　）
    A．是奇函数B．是偶函数
    C．既是奇函数，又是偶函数D．是非奇非偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某村欲修建一横断面为等腰梯形的水渠（如图），为降低成本，必须尽量减少水与水渠壁的接触面，若水渠的横断面面积设计为定值m，渠深3米，则水渠侧壁的倾斜角α应为多少时，方能使修建成本最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

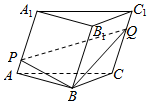    10．如图，设三棱柱ABC-A1B1C1的体积为2，P、Q分别是侧棱AA1、CC1上的点，且AP=QC1，则四棱锥B-APQC的体积为$\frac{2}{3}$．

    查看答案和解析>>

    同步练习册答案