
| A�� | $\frac{{3\sqrt{26}}}{13}$ | B�� | $\frac{{3\sqrt{5}}}{5}$ | C�� | $\frac{{\sqrt{6}}}{2}$ | D�� | $\frac{3}{2}$ |
���� ����ֱ�ߺ�Բ�ཻʱ���ҳ���ʽ���˫���������ʵĹ�ʽ����ת����⼴�ɣ�
��� 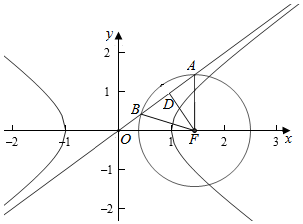 �⣺��˫���ߵ�һ������ΪF��c��0����˫���ߵ�һ��������Ϊy=$\frac{b}{a}$x����bx-ay=0��
�⣺��˫���ߵ�һ������ΪF��c��0����˫���ߵ�һ��������Ϊy=$\frac{b}{a}$x����bx-ay=0��
�ཹ�㵽�����ߵľ���d=$\frac{|bc|}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{bc}{c}=b$��
��|AF|=|BF|=a��
��|AD|=$\sqrt{A{F}^{2}-D{F}^{2}}$=$\sqrt{{a}^{2}-{b}^{2}}$��
��|AB|=2|AD|=2$\sqrt{{a}^{2}-{b}^{2}}$=$\frac{2}{3}$c��
ƽ����4��a2-b2��=$\frac{4}{9}$c2��
��a2-c2+a2=$\frac{1}{9}$c2��
��2a2=$\frac{10}{9}$c2��
��c2=$\frac{9}{5}$a2��
��c=$\frac{{3\sqrt{5}}}{5}$a��
��������e=$\frac{{3\sqrt{5}}}{5}$��
��ѡ��B
���� ������Ҫ����˫���������ʵļ��㣬����ֱ�ߺ�Բ�ཻ���ҳ���ʽ�������̹�ϵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��Ʒ��� | �� | �� | �� | �� | �� |
| ��ѹ��x�� | 10 | 15 | 20 | 25 | 30 |
| ������y�� | 0.6 | 0.8 | 1.4 | 1.2 | 1.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �·�x | 1 | 2 | 3 | 4 | 5 |
| �ϸ����y������ | 50 | 60 | 70 | 80 | 100 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 24 | C�� | 64 | D�� | 81 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A�� | x��y������� | |
| B�� | ��x=6ʱ��y�Ĺ���ֵΪ8.3 | |
| C�� | xÿ����һ����λ��y����0.95����λ | |
| D�� | �����㣨3��4.8���IJв�Ϊ0.56 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
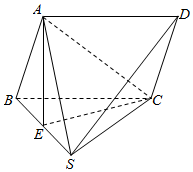 ��ͼ��������S-ABCD�У�����ABCD��ƽ���ı��Σ�ƽ��ABS��ƽ��CBS������SBC���������Σ�AB=AS����E��SB���е㣮
��ͼ��������S-ABCD�У�����ABCD��ƽ���ı��Σ�ƽ��ABS��ƽ��CBS������SBC���������Σ�AB=AS����E��SB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com