
| ��Ʒ��� | �� | �� | �� | �� | �� |
| ��ѹ��x�� | 10 | 15 | 20 | 25 | 30 |
| ������y�� | 0.6 | 0.8 | 1.4 | 1.2 | 1.5 |
���� ��1�������ݴ�����Ӧ�Ĺ�ʽ����������ع鷽�̣�
��2�������㣬��Ʒ���Ϊ�٢۵��Dz��ϸ�Ʒ������Ϊ�ϸ�Ʒ�����������2����������10�����������������һ���Ǻϸ�Ʒ��9����������ݸ��ʹ�ʽ���㼴�ɣ�
��� �⣺��1��b=$\frac{121-5��20}{2250-5��2{0}^{2}}$=0.044��
a=1.1-0.044��20=0.22��
���Իع�ֱ��$\hat y=0.044x+0.22$��
�ʵ���ѹ��Ϊ110��ʱ�����Ƶ���Ϊ5.06���࣬
��2����R=$\frac{U}{I}$�ɵã������ΪΪ$\frac{10}{0.6}$$\frac{50}{3}$��18��$\frac{15}{0.8}$=$\frac{75}{4}$��$\frac{20}{1.4}$=$\frac{100}{7}$��18��$\frac{25}{1.2}$=$\frac{125}{6}$��$\frac{30}{1.5}$=20
�����㣬��Ʒ���Ϊ�٢۵��Dz��ϸ�Ʒ������Ϊ�ϸ�Ʒ��
���������2����������10��������٢ڣ��٢ۣ��٢ܣ��٢ݣ��ڢۣ��ڢܣ��ڢݣ��ۢܣ��ۢݣ��ܢݣ�
����������һ���Ǻϸ�Ʒ��9�������
�������¼��ĸ���Ϊ$\frac{9}{10}$��
���� ���⿼���˻ع鷽�̺ŵ���ʵ����⣬�ؼ��ǻ����ù�ʽ�����ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
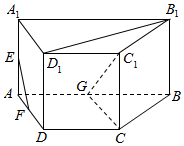 ��ͼ����ֱ������ABCD-A1B1C1D1�У�����ABCDΪ�������Σ�AB��CD��AD=DC=AA1=2��AB=4��E��F��G�ֱ�����AA1��AD��AB���е㣮
��ͼ����ֱ������ABCD-A1B1C1D1�У�����ABCDΪ�������Σ�AB��CD��AD=DC=AA1=2��AB=4��E��F��G�ֱ�����AA1��AD��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $\sqrt{5}$ | C�� | $\frac{2}{{\sqrt{5}}}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{3\sqrt{26}}}{13}$ | B�� | $\frac{{3\sqrt{5}}}{5}$ | C�� | $\frac{{\sqrt{6}}}{2}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�ĵ����������Σ�PA�͵���ABCD����PA=AD=2����M��N�ֱ���PD��PC�ϣ�2PN=NC��PM=MD
��ͼ��������P-ABCD�ĵ����������Σ�PA�͵���ABCD����PA=AD=2����M��N�ֱ���PD��PC�ϣ�2PN=NC��PM=MD�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com