
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 合格零件y(件) | 50 | 60 | 70 | 80 | 100 |
分析 (1)根据古典概型的概率公式进行计算即可.
(2)根据回归方程求出对应的回归系数进行估计即可.
解答 解:(1)由题意知本题是一个古典概型,设抽到相邻两个月的数据为事件A试验发生包含的事件是从5组数据中选取2组数据共有C52=10种情况,每种情况都是等
可能出现的其中,满足条件的事件是抽到相邻两个月的数据的情况有4种
∴P(A)=$\frac{4}{10}$=$\frac{2}{5}$; (4分)
(2)由数据求得$\overline{x}$=3,$\overline{y}$=72,$\sum_{i=1}^{5}$xiyi=1200,$\sum_{i=1}^{5}$xi2=55,
故$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$=$\frac{1200-5×3×72}{55-5×3×3}$=12,
∴$\widehat{a}$=$\overline{y}-\widehat{b}\overline{x}$=36,
∴y关于x的线性回归方程为$\widehat{y}$=12x+36,(10分)
当x=6,$\widehat{y}$=108(件),即预测该工人第6个月生产的合格零件的件数为108件.(12分)
点评 本题主要考查线线性回归的应用,考查学生的计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{26}}}{13}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{6}$或$\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
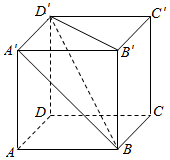 如图所示,在棱长为2的正方体ABCD-A′B′C′D′中,求:
如图所示,在棱长为2的正方体ABCD-A′B′C′D′中,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com