
分析 因为焦点在x轴上的双曲线的两条渐近线方程为y=±$\frac{b}{a}$x,焦点在y轴上的双曲线两条渐近线方程为y=±$\frac{a}{b}$x,所以分情况讨论a,b的关系,再根据a,b求出c,利用离心率e=$\frac{c}{a}$,就可求出双曲线的离心率.
解答 解:当双曲线焦点在x轴上时,两条渐近线方程为y=±$\frac{b}{a}$x,
又∵已知两条渐近线方程为y=±2x,∴$\frac{b}{a}$=2,b=2a
∴c=$\sqrt{5}$a,离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}a}{a}$=$\sqrt{5}$
当双曲线焦点在y轴上时,两条渐近线方程为y=±$\frac{a}{b}$x,
又∵已知两条渐近线方程为y=±2x,∴$\frac{a}{b}$=2,a=2b
∴c=$\sqrt{5}$b,离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}b}{2b}$=$\frac{\sqrt{5}}{2}$
故答案为:$\sqrt{5}$或$\frac{\sqrt{5}}{5}$
点评 本题主要考查了双曲线的离心率的求法,关键是求a,c的关系,注意对双曲线的焦点的位置进行讨论.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X=i | 0 | 1 | 2 | 3 |
| P(X=i) | $\frac{1}{4}$ | a | $\frac{1}{4}$ | b |
| A. | $\frac{1}{24}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
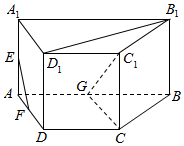 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AD=DC=AA1=2,AB=4,E、F、G分别是棱AA1、AD、AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AD=DC=AA1=2,AB=4,E、F、G分别是棱AA1、AD、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{26}}}{13}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
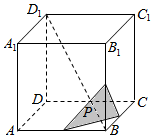 如图,在正方体ABCD-A1B1C1D1中,AB=1,点P为BD1上一点,平面α满足:点P∈平面α,直BD1⊥平面α,设以B为顶点,以连接平面α与正方体棱的交点为底面的几何体的体积为V,则V的最大值为( )
如图,在正方体ABCD-A1B1C1D1中,AB=1,点P为BD1上一点,平面α满足:点P∈平面α,直BD1⊥平面α,设以B为顶点,以连接平面α与正方体棱的交点为底面的几何体的体积为V,则V的最大值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{16}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com