练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．解方程：$\sqrt{x}$+$\sqrt{x+5}$+2$\sqrt{{x}^{2}+5x}$=25-2x．

    分析 构造函数y=$\sqrt{x}$+$\sqrt{x+5}$+2$\sqrt{{x}^{2}+5x}$y=25-2x．判断y=$\sqrt{x}$+$\sqrt{x+5}$+2$\sqrt{{x}^{2}+5x}$为增函数，y=25-2x．减函数，利用开方判断即可．

    解答 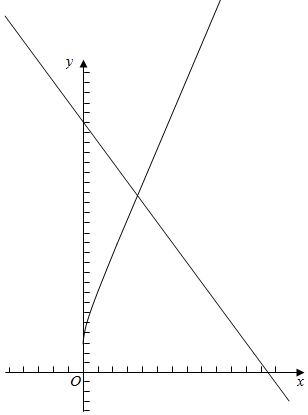解：y=$\sqrt{x}$+$\sqrt{x+5}$+2$\sqrt{{x}^{2}+5x}$
    y=25-2x．

    根据函数的单调性得出：y=$\sqrt{x}$+$\sqrt{x+5}$+2$\sqrt{{x}^{2}+5x}$为增函数，
    y=25-2x．减函数，
    交点只有一个，
    所以方程：$\sqrt{x}$+$\sqrt{x+5}$+2$\sqrt{{x}^{2}+5x}$=25-2x．只有一个根．
    x=4方程成立，

    点评 本题考查了函数的思想，方程的求解，利用函数图象求解问题，关键发现特殊值的验证．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．如图，已四棱锥P-ABCD的底面是正方形，PA⊥底面ABCD，且PA=AD=2，点M、N分别在PD、PC上，2PN=NC，PM=MD
    （1）求证：PC⊥平面AMN；
    （2）求四面体P-ABN的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某村欲修建一横断面为等腰梯形的水渠（如图），为降低成本，必须尽量减少水与水渠壁的接触面，若水渠的横断面面积设计为定值m，渠深3米，则水渠侧壁的倾斜角α应为多少时，方能使修建成本最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知$\overrightarrow{a}$为非零向量，$\overrightarrow{b}$=（3，4），且$\overrightarrow{a}$⊥$\overrightarrow{b}$，求$\overrightarrow{a}$的单位向量$\overrightarrow{{a}_{0}}$=（$\frac{4}{5}$，-$\frac{3}{5}$）或（-$\frac{4}{5}$，$\frac{3}{5}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在8和200之间插入三个数，使它们构成等比数列，求这三个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值．
    $\overrightarrow x$$\overrightarrow y$$\overrightarrow w$ $\sum_{i=1}^8{\;}$（x1-$\overrightarrow x$）2$\sum_{i=1}^8{\;}$（w1-$\overrightarrow w$）2$\sum_{i=1}^8{\;}$（x1-$\overrightarrow x$）（y-$\overrightarrow y$）$\sum_{i=1}^8{\;}$（w1-$\overrightarrow w$）（y-$\overrightarrow y$）
    46.656.36.8289.81.61469108.8
    表中${w_i}=\sqrt{x_i}$，$\overrightarrow w$=$\frac{1}{8}$$\sum_{i=1}^8{w_i}$
    （Ⅰ）根据散点图判断，y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
    （Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
    （Ⅲ）以知这种产品的年利率z与x、y的关系为z=0.2y-x．根据（Ⅱ）的结果回答
    当年宣传费x=49时，年销售量及年利润的预报值是多少？
    附：对于一组数据（u1 v1），（u2 v2）…..（un vn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：$\widehatβ=\frac{{\sum_{i=1}^n{（{u_i}-\overline u）（{v_i}-\overline v）}}}{{\sum_{i=1}^n{{{（{u_i}-\overline u）}^2}}}}，\widehatα=\overline v-\widehatβ\overline u$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

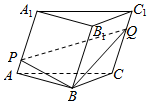    10．如图，设三棱柱ABC-A1B1C1的体积为2，P、Q分别是侧棱AA1、CC1上的点，且AP=QC1，则四棱锥B-APQC的体积为$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在正六棱锥P-ABCDEF中，AB=1，若平面PAB⊥平面PDE，则PA=$\frac{{\sqrt{7}}}{2}$，该正六棱锥的体积是$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．观察下列等式
    l+2+3+…+n=$\frac{1}{2}$n（n+l）；
    l+3+6+…+$\frac{1}{2}$n（n+1）=$\frac{1}{6}$n（n+1）（n+2）；
    1+4+10+…$\frac{1}{6}$n（n+1）（n+2）=$\frac{1}{24}$n（n+1）（n+2）（n+3）；
    可以推测，1+5+15+…+$\frac{1}{24}$n（n+1）（n+2）（n+3）=$\frac{1}{120}$n（n+1）（n+2）（n+3）（n+4），（n∈N*）．

    查看答案和解析>>

    同步练习册答案