
 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为 ,车速为
,车速为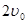 (水流速度忽略不计).
(水流速度忽略不计).
 ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间.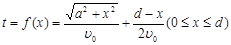 .……3分
.……3分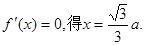 ……………………………………………………5分
……………………………………………………5分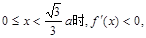 …………………………………………………6分
…………………………………………………6分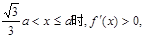 ……………………………………………………7分
……………………………………………………7分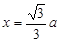 时,所用的时间最短,最短时间为:
时,所用的时间最短,最短时间为: .………………………………9分
.………………………………9分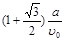 .
.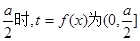 上的减函数,所以当
上的减函数,所以当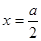 时,
时,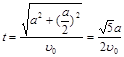 ………………………………………………14分
………………………………………………14分 时,该学生从家出发到达学校所用的最短时间是
时,该学生从家出发到达学校所用的最短时间是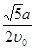


科目:高中数学 来源:不详 题型:解答题
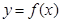 的图像(如图所示)过点
的图像(如图所示)过点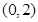 、
、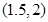 和点
和点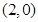 ,且函数图像关于点
,且函数图像关于点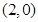 对称;直线
对称;直线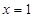 和
和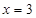 及
及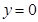 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数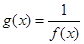 的相关性质与图像,
的相关性质与图像, 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间; 的大致图像(要充分反映由图像及条件给出的信息);
的大致图像(要充分反映由图像及条件给出的信息);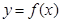 的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,其中
,其中 .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,求
时,求 的单调区间;
的单调区间; 在区间
在区间 内均存在零点.
内均存在零点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com