
【题目】今年情况特殊,小王在居家自我隔离时对周边的水产养殖产业进行了研究.![]() 、
、![]() 两个投资项目的利润率分别为投资变量
两个投资项目的利润率分别为投资变量![]() 和
和![]() .根据市场分析,
.根据市场分析,![]() 和
和![]() 的分布列分别为:
的分布列分别为:
| 5% | 10% | ||
| 0.8 | 0.2 | ||
| 2% | 8% | 12% | |
| 0.2 | 0.5 | 0.3 | |
(1)若在![]() 两个项目上各投资
两个项目上各投资![]() 万元,
万元,![]() 和
和![]() 分别表示投资项目
分别表示投资项目![]() 和
和![]() 所获得的利润,求方差
所获得的利润,求方差![]() ,
,![]() ;
;
(2)若在![]() 两个项目上共投资
两个项目上共投资![]() 万元,那么如何分配,能使投资
万元,那么如何分配,能使投资![]() 项目所得利润的方差与投资
项目所得利润的方差与投资![]() 项目所得利润的方差的和最小,最小值是多少?
项目所得利润的方差的和最小,最小值是多少?
(注:![]() )
)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个结论:
,有下列四个结论:
①![]() 为偶函数;②
为偶函数;②![]() 的值域为
的值域为![]() ;
;
③![]() 在
在![]() 上单调递减;④
上单调递减;④![]() 在
在![]() 上恰有8个零点,
上恰有8个零点,
其中所有正确结论的序号为( )
A.①③B.②④C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
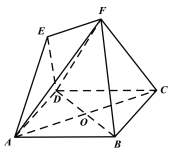
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的焦点为
)的焦点为![]() ,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆E的方程;
(2)过点F的直线l交椭圆E于M,N两点,点P的坐标为![]() ,直线
,直线![]() 与x轴交于A点,直线
与x轴交于A点,直线![]() 与x轴交于B点,求证:
与x轴交于B点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 过点
过点![]() ,
,![]() ,
,![]() 是两个焦点.以椭圆
是两个焦点.以椭圆![]() 的上顶点
的上顶点![]() 为圆心作半径为
为圆心作半径为![]() 的圆,
的圆,
(1)求椭圆![]() 的方程;
的方程;
(2)存在过原点的直线![]() ,与圆
,与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),使得
上),使得![]() ,求圆
,求圆![]() 半径
半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.
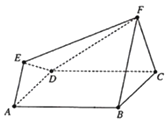
(1)证明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com