
【题目】已知椭圆E:![]() (
(![]() )的焦点为
)的焦点为![]() ,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆E的方程;
(2)过点F的直线l交椭圆E于M,N两点,点P的坐标为![]() ,直线
,直线![]() 与x轴交于A点,直线
与x轴交于A点,直线![]() 与x轴交于B点,求证:
与x轴交于B点,求证:![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据直线与圆相切列出对应方程,再结合椭圆的基本知识计算求解即可;
(2)先讨论l与y轴重合时的情况,再在l与y轴不重合的情况下,设![]() ,
,![]() ,l的方程为
,l的方程为![]() ,将之与椭圆方程联立,得到韦达定理.解法一:利用韦达定理化简证明
,将之与椭圆方程联立,得到韦达定理.解法一:利用韦达定理化简证明![]() ,从而证明出
,从而证明出![]() ;解法二:设
;解法二:设![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() :
:![]() ,然后根据方程求出
,然后根据方程求出![]() ,再结合韦达定理证明
,再结合韦达定理证明![]() ,从而证明出
,从而证明出![]() .
.
(1)由已知得![]() ,
,![]() ,因此
,因此![]() ,
,
所以椭圆E的方程为![]() .
.
(2)解法一:
①当l与y轴重合时,由题意知![]() .
.
②当l与y轴不重合时,设l的方程为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
直线![]() ,
,![]() 的斜率之和为
的斜率之和为![]() ,
,
由![]() ,
,![]() 得
得![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
![]() ,
,
所以![]() ,
,![]() ,
,
所以![]()
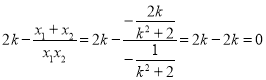 ,
,
从而![]() ,故
,故![]() ,
,![]() 的倾斜角互补,
的倾斜角互补,
所以![]() ,因此
,因此![]() .
.
综上所述,![]() .
.
解法二:
①当l与y轴重合时,由题意知![]() .
.
②当l与y轴不重合时,设l的方程为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
将![]() 代入
代入![]() 得
得![]() .
.
![]() ,
,
所以![]() ,
,![]() .
.
设![]() :
:![]() ,
,![]() :
:![]() ,
,![]() ,
,![]()
易知![]() ,
,![]() ,
,
在![]() 中,令
中,令![]() 得
得![]() ,
,
在![]() 中,令
中,令![]() 得
得![]() ,
,
于是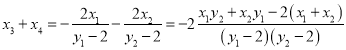 ,
,
由![]() ,
,![]() 得
得
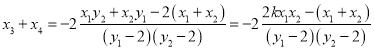 ,
,
由于![]() ,因此
,因此![]() ,
,
所以点A与点B关于原点O对称,
而点P在y轴上,因此![]() .
.
综上所述,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() 是定义域为
是定义域为![]() 的偶函数,对
的偶函数,对![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() ,函数
,函数![]() .现给出以下命题:①
.现给出以下命题:①![]() 是周期函数;②
是周期函数;②![]() 的图象关于直线
的图象关于直线![]() 对称;③当
对称;③当![]() 时,
时,![]() 在
在![]() 内有一个零点;④当
内有一个零点;④当![]() 时,
时,![]() 在
在![]() 上至少有六个零.其中正确命题的序号为________.
上至少有六个零.其中正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年情况特殊,小王在居家自我隔离时对周边的水产养殖产业进行了研究.![]() 、
、![]() 两个投资项目的利润率分别为投资变量
两个投资项目的利润率分别为投资变量![]() 和
和![]() .根据市场分析,
.根据市场分析,![]() 和
和![]() 的分布列分别为:
的分布列分别为:
| 5% | 10% | ||
| 0.8 | 0.2 | ||
| 2% | 8% | 12% | |
| 0.2 | 0.5 | 0.3 | |
(1)若在![]() 两个项目上各投资
两个项目上各投资![]() 万元,
万元,![]() 和
和![]() 分别表示投资项目
分别表示投资项目![]() 和
和![]() 所获得的利润,求方差
所获得的利润,求方差![]() ,
,![]() ;
;
(2)若在![]() 两个项目上共投资
两个项目上共投资![]() 万元,那么如何分配,能使投资
万元,那么如何分配,能使投资![]() 项目所得利润的方差与投资
项目所得利润的方差与投资![]() 项目所得利润的方差的和最小,最小值是多少?
项目所得利润的方差的和最小,最小值是多少?
(注:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平
近似为样本平
均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)央视媒体平台从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.附:
的人数是Y,求变量Y的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并解答.
①![]()
②![]()
③![]() 的面积为
的面积为![]()
在![]() 中,内角A,B,C所对的边分别为a,b,c,已知b-c=2,cosA=
中,内角A,B,C所对的边分别为a,b,c,已知b-c=2,cosA=![]() , .
, .
(1)求a;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采购经理指数(PMI)是衡量一个国家制造业的“体检表”,是衡量制造业在生产新订单、商品价格、存货、雇员、订单交货、新出口订单和进口等八个方面状况的指数,下图为2018年9月—2019年9月我国制造业的采购经理指数(单位:%).
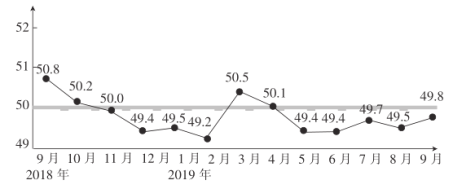
(1)求2019年前9个月我国制造业的采购经理指数的中位数及平均数(精确到0.1);
(2)从2019年4月—2019年9月这6个月任意选取2个月,求这两个月至少有一个月采购经理指数与上个月相比有所回升的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com