
【题目】已知![]() 是定义域为
是定义域为![]() 的偶函数,对
的偶函数,对![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() ,函数
,函数![]() .现给出以下命题:①
.现给出以下命题:①![]() 是周期函数;②
是周期函数;②![]() 的图象关于直线
的图象关于直线![]() 对称;③当
对称;③当![]() 时,
时,![]() 在
在![]() 内有一个零点;④当
内有一个零点;④当![]() 时,
时,![]() 在
在![]() 上至少有六个零.其中正确命题的序号为________.
上至少有六个零.其中正确命题的序号为________.
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】设数列:A:a1,a2,…,an,B:b1,b2,…,bn.已知ai,bj∈{0,1}(i=1,2,…,n;j=1,2,…,n),定义n×n数表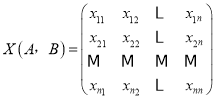 ,其中xij
,其中xij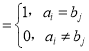 .
.
(1)若A:1,1,1,0,B:0,1,0,0,写出X(A,B);
(2)若A,B是不同的数列,求证:n×n数表X(A,B)满足“xij=xji(i=1,2,…,n;j=1,2,…,n;i![]() j)”的充分必要条件为“ak+bk=1(k=1,2,…,n)”;
j)”的充分必要条件为“ak+bk=1(k=1,2,…,n)”;
(3)若数列A与B中的1共有n个,求证:n×n数表X(A,B)中1的个数不大于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
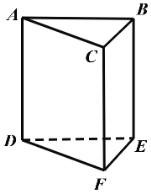
【题目】如图,一颗棋子从三棱柱的一个项点沿棱移到相邻的另一个顶点的概率均为![]() ,刚开始时,棋子在上底面点
,刚开始时,棋子在上底面点![]() 处,若移了
处,若移了![]() 次后,棋子落在上底面顶点的概率记为
次后,棋子落在上底面顶点的概率记为![]() .
.
(1)求![]() ,
,![]() 的值:
的值:
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
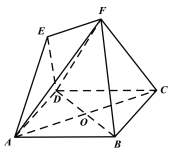
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的焦点为
)的焦点为![]() ,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆E的方程;
(2)过点F的直线l交椭圆E于M,N两点,点P的坐标为![]() ,直线
,直线![]() 与x轴交于A点,直线
与x轴交于A点,直线![]() 与x轴交于B点,求证:
与x轴交于B点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一条曲线C在y轴右侧,曲线C上任意一点到点![]() 的距离减去它到y轴的距离都等于1.
的距离减去它到y轴的距离都等于1.
(1)求曲线C的方程;
(2)直线![]() 与轨迹C交于A,B两点,问:在x轴上是否存在定点
与轨迹C交于A,B两点,问:在x轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 关于x轴对称而与直线
关于x轴对称而与直线![]() 的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com