
【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
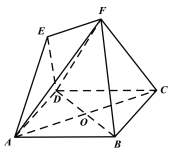
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,有下述四个结论:
,有下述四个结论:
①![]() 是周期为
是周期为![]() 的函数;
的函数;
②![]() 在
在![]() 单调递增;
单调递增;
③![]() 在
在![]() 上有三个零点;
上有三个零点;
④![]() 的值域是
的值域是![]() .
.
其中所有正确结论的编号是( )
A.②③B.①③C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的焦点为
)的焦点为![]() ,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆E的方程;
(2)过点F的直线l交椭圆E于M,N两点,点P的坐标为![]() ,直线
,直线![]() 与x轴交于A点,直线
与x轴交于A点,直线![]() 与x轴交于B点,求证:
与x轴交于B点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() 、
、![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() (不与
(不与![]() 轴重合)交椭圆
轴重合)交椭圆![]() 于
于![]() 、
、![]() 点,直线
点,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() .
.
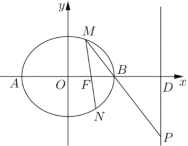
(1)求椭圆![]() 的方程;
的方程;
(2)若![]()
![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com