
【题目】已知椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() 、
、![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() (不与
(不与![]() 轴重合)交椭圆
轴重合)交椭圆![]() 于
于![]() 、
、![]() 点,直线
点,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() .
.
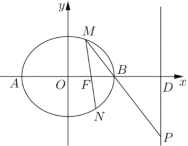
(1)求椭圆![]() 的方程;
的方程;
(2)若![]()
![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
科目:高中数学 来源: 题型:
【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并解答.
①![]()
②![]()
③![]() 的面积为
的面积为![]()
在![]() 中,内角A,B,C所对的边分别为a,b,c,已知b-c=2,cosA=
中,内角A,B,C所对的边分别为a,b,c,已知b-c=2,cosA=![]() , .
, .
(1)求a;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意![]() ,给定区间
,给定区间![]() ,设函数
,设函数![]() 表示实数
表示实数![]() 与
与![]() 所属的给定区间内唯一整数之差的绝对值.
所属的给定区间内唯一整数之差的绝对值.
(1)当![]() 时,求出
时,求出![]() 的解析式;
的解析式;![]() 时,写出绝对值符号表示的
时,写出绝对值符号表示的![]() 解析式;
解析式;
(2)求![]() ,
,![]() ,判断函数
,判断函数![]() 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(3)当![]() 时,求方程
时,求方程![]() 的实根.(要求说明理由,
的实根.(要求说明理由,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,椭圆
,椭圆![]() 上的点到其左焦点
上的点到其左焦点![]() 的最大距离为
的最大距离为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最小值和此时直线
的最小值和此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采购经理指数(PMI)是衡量一个国家制造业的“体检表”,是衡量制造业在生产新订单、商品价格、存货、雇员、订单交货、新出口订单和进口等八个方面状况的指数,下图为2018年9月—2019年9月我国制造业的采购经理指数(单位:%).
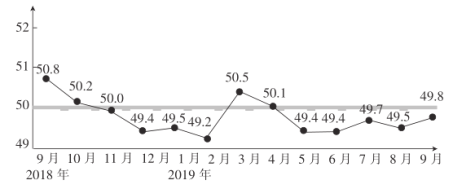
(1)求2019年前9个月我国制造业的采购经理指数的中位数及平均数(精确到0.1);
(2)从2019年4月—2019年9月这6个月任意选取2个月,求这两个月至少有一个月采购经理指数与上个月相比有所回升的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 过点
过点![]() 且渐近线为
且渐近线为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A.曲线![]() 的方程为
的方程为![]() ;
;
B.左焦点到一条渐近线距离为![]() ;
;
C.直线![]() 与曲线
与曲线![]() 有两个公共点;
有两个公共点;
D.过右焦点截双曲线所得弦长为![]() 的直线只有三条;
的直线只有三条;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧面PAD⊥底面ABCD,E为PA的中点,过C,D,E三点的平面与PB交于点F,且PA=PD=AB=2.
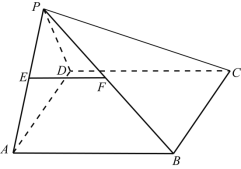
(1)证明:![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,则在线段
,则在线段![]() 上是否存在点G,使得二面角
上是否存在点G,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com