
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
(1)求出导数后,对![]() 分类讨论,利用导数可求得函数的单调区间;
分类讨论,利用导数可求得函数的单调区间;
(2)分离参数后得![]() 在
在![]() 上恒成立,再构造函数利用导数求出最大值即可得到答案.
上恒成立,再构造函数利用导数求出最大值即可得到答案.
(1) ,
,
由定义域为![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,递增区间为
,递增区间为![]() ;
;
当![]() 时,令
时,令![]() ,则
,则![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,![]() 恒成立,
恒成立,
所以函数![]() 的递增区间为
的递增区间为![]() ,无减区间;
,无减区间;
当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() 或
或![]() ,由
,由![]() ,得
,得![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,递增区间为
,递增区间为![]() 和
和![]() ;
;
当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() 或
或![]() ,由
,由![]() ,得
,得![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,递增区间为
,递增区间为![]() 和
和![]() .
.
综上,当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,递增区间为
,递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ,无减区间;
,无减区间;
当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,递增区间为
,递增区间为![]() 和
和![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,递增区间为
,递增区间为![]() 和
和![]() .
.
(2)依题意得,![]() 在
在![]() 恒成立.
恒成立.
①当![]() 时,不等式显然成立;
时,不等式显然成立;
②当![]() 时,
时,![]() ,即
,即![]() 成立,
成立,
设![]() ,则
,则 ,
,
设![]() ,则
,则![]() 在
在![]() 单调递减,
单调递减,![]() ,
,
所以,当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减.
单调递减.
所以![]()
所以![]() ,解得
,解得![]() .
.
综上,当![]() 时,
时,![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】如图,一颗棋子从三棱柱的一个项点沿棱移到相邻的另一个顶点的概率均为![]() ,刚开始时,棋子在上底面点
,刚开始时,棋子在上底面点![]() 处,若移了
处,若移了![]() 次后,棋子落在上底面顶点的概率记为
次后,棋子落在上底面顶点的概率记为![]() .
.
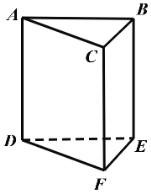
(1)求![]() ,
,![]() 的值:
的值:
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
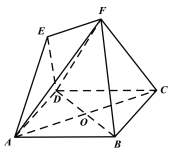
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的焦点为
)的焦点为![]() ,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆E的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆E的方程;
(2)过点F的直线l交椭圆E于M,N两点,点P的坐标为![]() ,直线
,直线![]() 与x轴交于A点,直线
与x轴交于A点,直线![]() 与x轴交于B点,求证:
与x轴交于B点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 过点
过点![]() ,
,![]() ,
,![]() 是两个焦点.以椭圆
是两个焦点.以椭圆![]() 的上顶点
的上顶点![]() 为圆心作半径为
为圆心作半径为![]() 的圆,
的圆,
(1)求椭圆![]() 的方程;
的方程;
(2)存在过原点的直线![]() ,与圆
,与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),使得
上),使得![]() ,求圆
,求圆![]() 半径
半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一条曲线C在y轴右侧,曲线C上任意一点到点![]() 的距离减去它到y轴的距离都等于1.
的距离减去它到y轴的距离都等于1.
(1)求曲线C的方程;
(2)直线![]() 与轨迹C交于A,B两点,问:在x轴上是否存在定点
与轨迹C交于A,B两点,问:在x轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 关于x轴对称而与直线
关于x轴对称而与直线![]() 的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是
是![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 分别关于两坐标轴及坐标原点的对称点,平行于
分别关于两坐标轴及坐标原点的对称点,平行于![]() 的直线
的直线![]() 交
交![]() 于异于
于异于![]() 的两点
的两点![]() .点
.点![]() 关于原点的对称点为
关于原点的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴围成的三角形是等腰三角形.
轴围成的三角形是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com