【题目】已知函数f（x）＝|2x﹣1|﹣3|x+1|，设f（x）的最大值为M.
（1）求M；
（2）若正数a，b满足
Mab，证明：a4b+ab4
.
【答案】（1）M＝3（2）证明见解析；
【解析】
（1）由f（x）＝|2x﹣1|﹣3|x+1|＝|2x﹣1|﹣|2x+2|﹣|x+1|，结合绝对值不等式的性质和绝对值的几何意义，可得所求最大值；
（2）由（1）可得
3ab，a4b+ab4＝ab（a3+b3）
（
）（a3+b3），再由基本不等式即可得证.
解：（1）函数f（x）＝|2x﹣1|﹣3|x+1|
＝|2x﹣1|﹣|2x+2|﹣|x+1|≤|2x﹣1﹣2x﹣2|﹣|﹣1+1|＝3，
当x＝﹣1时，f（x）取得最大值3，即M＝3；
（2）证明：正数a，b满足3ab，
故a4b+ab4＝ab（a3+b3）（）（a3+b3）（1+1
）
（2+2
）
，当且仅当a＝b
时等号成立，
故a4b+ab4
.
口算小状元口算速算天天练系列答案科目：高中数学 来源： 题型：
【题目】今年情况特殊，小王在居家自我隔离时对周边的水产养殖产业进行了研究．
、
两个投资项目的利润率分别为投资变量
和
．根据市场分析，和的分布列分别为：
| 5% | 10% | ||
| 0.8 | 0.2 | ||
| 2% | 8% | 12% | |
| 0.2 | 0.5 | 0.3 | |
（1）若在
两个项目上各投资
万元，
和
分别表示投资项目和所获得的利润，求方差
，
；
（2）若在两个项目上共投资
万元，那么如何分配，能使投资项目所得利润的方差与投资项目所得利润的方差的和最小，最小值是多少？
（注：
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某项数学竞赛考试共四道题，考察内容分别为代数、几何、数论、组合，已知前两题每题满分40分，后两题每题满分60分，题目难度随题号依次递增，已知学生甲答题时，若该题会做则必得满分，若该题不会做则不作答得0分，通过对学生甲以往测试情况的统计，得到他在同类模拟考试中各题的得分率，如表所示：
假设学生甲每次考试各题的得分相互独立.
（1）若此项竞赛考试四道题的顺序依次为代数、几何、数论、组合，试预测学生甲考试得160分的概率；
（2）学生甲研究该项竞赛近五年的试题发现第1题都是代数题，于是他在赛前针对代数版块进行了强化训练，并取得了很大进步，现在，只要代数题是在试卷第1、2题的位置，他就一定能答对，若今年该项数学竞赛考试四道题的顺序依次为代数、数论、组合、几何，试求学生甲此次考试得分X的分布列.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】请从下面三个条件中任选一个，补充在下面的横线上，并解答．
①
②
③
的面积为
在中，内角A，B，C所对的边分别为a，b，c，已知b－c=2，cosA=
， ．
（1）求a；
（2）求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在
中，
，
，
，
分别为
，
的中点
是由
绕直线
旋转得到，连结
，
，
.
（1）证明：
平面
；
（2）若
，棱
上是否存在一点
，使得
？若存在，确定点 的位置；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对任意
，给定区间
，设函数
表示实数
与所属的给定区间内唯一整数之差的绝对值.
（1）当
时，求出的解析式；
时，写出绝对值符号表示的解析式；
（2）求
，
，判断函数
的奇偶性，并证明你的结论；
（3）当
时，求方程
的实根.（要求说明理由，
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
指数是用体重公斤数除以身高米数的平方得出的数字，是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准．对于高中男体育特长生而言，当数值大于或等于20.5时，我们说体重较重，当数值小于20.5时，我们说体重较轻，身高大于或等于
我们说身高较高，身高小于170cm我们说身高较矮．
（Ⅰ）已知某高中共有32名男体育特长生，其身高与
指数的数据如散点图，请根据所得信息，完成下述列联表，并判断是否有
的把握认为男生的身高对指数有影响．
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
（Ⅱ）①从上述32名男体育特长生中随机选取8名，其身高和体重的数据如表所示：
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为
．利用已经求得的线性回归方程，请完善下列残差表，并求
（解释变量（身高）对于预报变量（体重）变化的贡献值）（保留两位有效数字）；
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重（kg） | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 |
|
|
|
|
|
|
|
②通过残差分析，对于残差的最大（绝对值）的那组数据，需要确认在样本点的采集中是否有人为的错误，已知通过重新采集发现，该组数据的体重应该为
．小明重新根据最小二乘法的思想与公式，已算出
，请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程．
参考数据：
，
，
，
，
参考公式：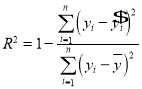
，
，
，
，
．
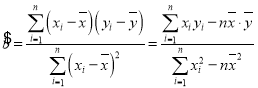| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
