
分析 (1)化简复数z1,求出$\overline{{z}_{1}}$与|z1|的值;
(2)设复数z=x+yi,x、y∈R,求出点z的轨迹是单位圆,画出图形,结合图形求出|z-z1|的最值即可.
解答  解:∵复数z1=i(1+i)2=i(1+2i-1)=2i2=-2,
解:∵复数z1=i(1+i)2=i(1+2i-1)=2i2=-2,
(1)∴$\overline{{z}_{1}}$=-2,
|z1|=2;
(2)设复数z=x+yi,x、y∈R,
∵|z+3-4i|=1,
∴|(x+3)+(y-4)i|=1,
∴(x+3)2+(y-4)2=1,
它表示圆心为P(-3,4),半径为1的圆;
画出图形,如图所示;
则圆心P到复数z1点A的距离为
|PA|=$\sqrt{{(-3+2)}^{2}{+4}^{2}}$=$\sqrt{17}$,
所以|z-z1|的最大值为|PA|+r=$\sqrt{17}$+1,
最小值为|PA|-r=$\sqrt{17}$-1.
点评 本题考查了复数的概念与代数运算问题,也考查了求轨迹方程的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 利润y | 5.8 | 6.6 | 7.1 | 7.4 | 8.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | B. | [kπ+$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z | ||
| C. | [2kπ+$\frac{5π}{12}$,2kπ+$\frac{11π}{12}$],k∈Z | D. | [2kπ-$\frac{π}{12}$,2kπ+$\frac{5π}{12}$],k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2-$\sqrt{3}$ | D. | -5 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:解答题
已知函数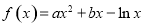 (
(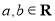 ).
).
(1)当 时,求函数
时,求函数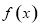 在
在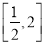 上的最大值和最小值;
上的最大值和最小值;
(2)当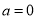 时,是否存在正实数
时,是否存在正实数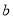 ,当
,当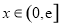 (
(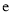 是自然对数底数)时,函数
是自然对数底数)时,函数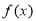 的最小值是3,若存在,求出
的最小值是3,若存在,求出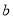 的值;若不存在,说明理由;
的值;若不存在,说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com