
已知函数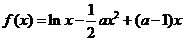 (
(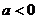 ).
).
(Ⅰ)求函数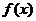 的单调区间;
的单调区间;
(Ⅱ)记函数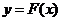 的图象为曲线
的图象为曲线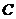 .设点
.设点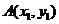 ,
, 是曲线
是曲线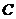 上的不同两点.如果在曲线
上的不同两点.如果在曲线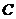 上存在点
上存在点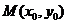 ,使得:①
,使得:①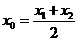 ;②曲线
;②曲线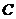 在点
在点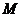 处的切线平行于直线
处的切线平行于直线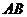 ,则称函数
,则称函数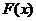 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数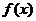 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
解:(Ⅰ)易知函数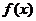 的定义域是
的定义域是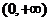 ,
,
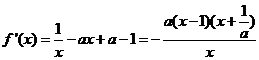 .…………1分
.…………1分
①当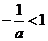 时,即
时,即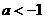 时, 令
时, 令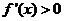 ,解得
,解得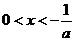 或
或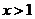 ;
;
令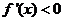 ,解得
,解得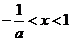 .……………2分
.……………2分
所以,函数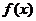 在
在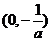 和
和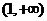 上单调递增,在
上单调递增,在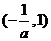 上单调递减
上单调递减
②当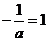 时,即
时,即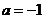 时, 显然,函数
时, 显然,函数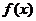 在
在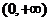 上单调递增;……………3分
上单调递增;……………3分
③当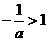 时,即
时,即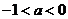 时, 令
时, 令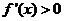 ,解得
,解得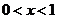 或
或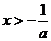 ;
;
令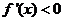 ,解得
,解得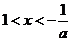 .……………4分
.……………4分
所以,函数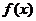 在
在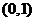 和
和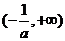 上单调递增,在
上单调递增,在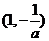 上单调递减
上单调递减
综上所述,
⑴当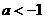 时,函数
时,函数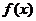 在
在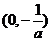 和
和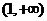 上单调递增,在
上单调递增,在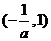 上单调递减;
上单调递减;
⑵当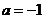 时,函数
时,函数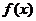 在
在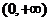 上单调递增;
上单调递增;
⑶当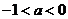 时,函数
时,函数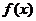 在
在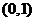 和
和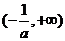 上单调递增,在
上单调递增,在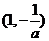 上单调递减.……………5分
上单调递减.……………5分
(Ⅱ)假设函数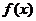 存在“中值相依切线”.
存在“中值相依切线”.
设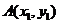 ,
,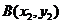 是曲线
是曲线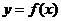 上的不同两点,且
上的不同两点,且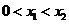 ,
,
则 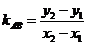
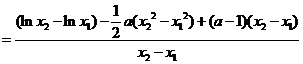
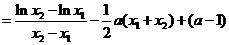 ……………7分
……………7分
曲线在点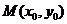 处的切线斜率
处的切线斜率
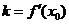
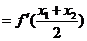
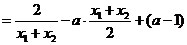 ,……………8分
,……………8分
依题意得: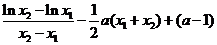
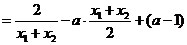 .
.
化简可得: 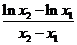
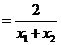 ,即
,即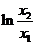 =
=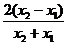
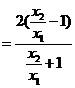 .
……………10分
.
……………10分
设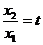 (
(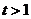 ),上式化为:
),上式化为: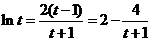 , 即
, 即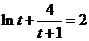 .
………12分
.
………12分
令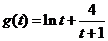 ,
,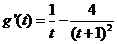
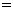
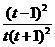 .
.
因为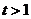 ,显然
,显然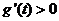 ,所以
,所以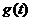 在
在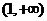 上递增,显然有
上递增,显然有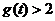 恒成立.
恒成立.
所以在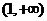 内不存在
内不存在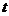 ,使得
,使得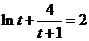 成立.
成立.
综上所述,假设不成立.所以,函数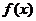 不存在“中值相依切线”.……………14分
不存在“中值相依切线”.……………14分


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| π |
| 24 |
| 5π |
| 24 |
| π |
| 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 11π |
| 6 |
| ||
| 2 |
| 3 |
| π |
查看答案和解析>>
科目:高中数学 来源: 题型:
| xn+2 | xn-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com