练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求下列函数的导数．

    y＝x·tan x；


    y′＝(x·tan x)′＝x′tan x＋x(tan x)′

    ＝tan x＋.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)＝

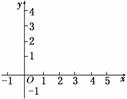
    (1)在如图所示给定的直角坐标系内画出f(x)的图像；

    (2)写出f(x)的单调递增区间；

    (3)由图像指出当x取什么值时f(x)有最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝－|x－5|＋2x－1的零点所在的区间是(　　)

    A．(0,1)                                              B．(1,2)

    C．(2,3)                                              D．(3,4)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某商家一月份至五月份累计销售额达3 860万元，预测六月份销售额为500万元，七月份销售额比六月份递增x%，八月份销售额比七月份递增x%，九、十月份销售总额与七、八月份销售总额相等．若一月份至十月份销售总额至少达7 000万元，则x的最小值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)与g(x)是定义在R上的两个可导函数，若f(x)，g(x)满足f′(x)＝g′(x)，则f(x)与g(x)满足(　　)

    A．f(x)＝g(x)                                      B．f(x)＝g(x)＝0

    C．f(x)－g(x)为常数函数                     D．f(x)＋g(x)为常数函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝x＋eln x的单调递增区间为(　　)

    A．(0，＋∞)　　　　　　                  B．(－∞，0)

    C．(－∞，0)和(0，＋∞)                    D．R

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3－ax2－3x.

    (1)若f(x)在[1，＋∞)上是增函数，求实数a的取值范围；

    (2)若x＝3是f(x)的极值点，求f(x)的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    f(x)是定义在(0，＋∞)上的非负可导函数，且满足xf′(x)＋f(x)≤0，对任意正数a，b，若a<b，则必有(　　)

    A．af(b)≤bf(a)                                   B．bf(a)≤af(b)

    C．af(a)≤f(b)                                    D．bf(b)≤f(a)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝sin x＋cos x，x∈R.

    (1)求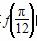的值；

    (2)试写出一个函数g(x)，使得g(x)f(x)＝cos 2x，并求g(x)的单调区间．

    查看答案和解析>>

    同步练习册答案