Question

10．若f（x）=x³+ax²+bx+c有两个极值点x₁，x₂且f（x₁）=x₁，则关于x的方程3[（f（x）]²+2af（x）+b=0的不同实根个数为（　　）

• A． 2
• B． 3
• C． 4
• D． 不确定

Answer 1

分析 由函数f（x）=x³+ax²+bx+c有两个极值点x₁，x₂，可得f′（x）=3x²+2ax+b=0有两个不相等的实数根，必有△=4a²-12b＞0．而方程3（f（x））²+2af（x）+b=0的△₁=△＞0，可知此方程有两解且f（x）=x₁或x₂．再分别讨论利用平移变换即可解出方程f（x）=x₁或f（x）=x₂解得个数．

解答 解：∵函数f（x）=x³+ax²+bx+c有两个极值点x₁，x₂，不妨设x₁＜x₂，
∴f′（x）=3x²+2ax+b=0有两个不相等的实数根，
∴△=4a²-12b＞0．解得x=$\frac{-a±\sqrt{{a}^{2}-3b}}{3}$．
∵x₁＜x₂，
∴x₁=$\frac{-a-\sqrt{{a}^{2}-3b}}{3}$，x₂=$\frac{-a+\sqrt{{a}^{2}-3b}}{3}$．
而方程3（f（x））²+2af（x）+b=0的△₁=△＞0，
∴此方程有两解且f（x）=x₁或x₂．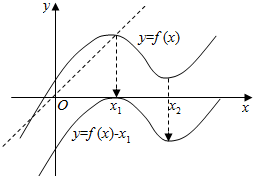
不妨取0＜x₁＜x₂，f（x₁）＞0．
①把y=f（x）向下平移x₁个单位即可得到y=f（x）-x₁的图象，
∵f（x₁）=x₁，可知方程f（x）=x₁有两解．
②把y=f（x）向下平移x₂个单位即可得到y=f（x）-x₂的图象，
∵f（x₁）=x₁，∴f（x₁）-x₂＜0，可知方程f（x）=x₂只有一解．
综上①②可知：方程f（x）=x₁或f（x）=x₂．只有3个实数解．
即关于x的方程3（f（x））²+2af（x）+b=0的只有3不同实根．
故选：B．

点评 本题综合考查了利用导数研究函数得单调性、极值及方程解得个数、平移变换等基础知识，考查了数形结合的思想方法、推理能力、分类讨论的思想方法、计算能力、分析问题和解决问题的能力．