
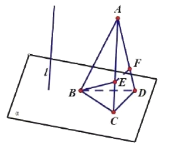
【题目】正四面体![]() 中,
中,![]() 在平面
在平面![]() 内,点
内,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 是平面
是平面![]() 的垂线,在该四面体绕
的垂线,在该四面体绕![]() 旋转的过程中,直线
旋转的过程中,直线![]() 与
与![]() 所成角为
所成角为![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】为了鼓励职员工作热情,某公司对每位职员一年来的工作业绩按月进行考评打分;年终按照职员的月平均值评选公司最佳职员并给予相应奖励.已知职员![]() 一年来的工作业绩分数的茎叶图如图所示:
一年来的工作业绩分数的茎叶图如图所示:
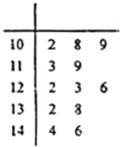
(1)根据职员![]() 的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
(2)由于职员![]() 的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员
的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员![]() 需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员
需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员![]() 获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年11月河南省三门峡市成功入围“十佳魅力中国城市”,吸引了大批投资商的目光,一些投资商积极准备投入到“魅力城市”的建设之中.某投资公司准备在2018年年初将四百万元投资到三门峡下列两个项目中的一个之中.
项目一:天坑院是黄土高原地域独具特色的民居形式,是人类“穴居”发展史演变的实物见证.现准备投资建设20个天坑院,每个天坑院投资0.2百万元,假设每个天坑院是否盈利是相互独立的,据市场调研,到2020年底每个天坑院盈利的概率为![]()
![]() ,若盈利则盈利投资额的40%,否则盈利额为0.
,若盈利则盈利投资额的40%,否则盈利额为0.
项目二:天鹅湖国家湿地公园是一处融生态、文化和人文地理于一体的自然山水景区.据市场调研,投资到该项目上,到2020年底可能盈利投资额的50%,也可能亏损投资额的30%,且这两种情况发生的概率分别为p和![]() .
.
(1)若投资项目一,记![]() 为盈利的天坑院的个数,求
为盈利的天坑院的个数,求![]() (用p表示);
(用p表示);
(2)若投资项目二,记投资项目二的盈利为![]() 百万元,求
百万元,求![]() (用p表示);
(用p表示);
(3)在(1)(2)两个条件下,针对以上两个投资项目,请你为投资公司选择一个项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 上各点的纵坐标伸长为原来的
上各点的纵坐标伸长为原来的![]() 倍(横坐标不变)得到曲线
倍(横坐标不变)得到曲线![]() ,求
,求![]() 的参数方程;
的参数方程;
(2)若![]() ,
,![]() 分别是直线
分别是直线![]() 与曲线
与曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,当
,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,当
,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,依此类推,一般地,当
,依此类推,一般地,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,其中
,其中![]() 、
、![]() 为常数,且
为常数,且![]() ,
,![]() .
.
(1)若![]() ,求数列
,求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若![]() ,问是否存在常数
,问是否存在常数![]() ,使得数列
,使得数列![]() 满足
满足![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若![]() ,设数列
,设数列![]() ,
,![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,墙上有一壁画,最高点![]() 离地面4米,最低点
离地面4米,最低点![]() 离地面2米,观察者从距离墙
离地面2米,观察者从距离墙![]() 米,离地面高
米,离地面高![]() 米的
米的![]() 处观赏该壁画,设观赏视角
处观赏该壁画,设观赏视角![]()
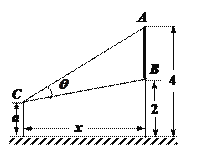
(1)若![]() 问:观察者离墙多远时,视角
问:观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() 当
当![]() 变化时,求
变化时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图数表:

每一行都是首项为1的等差数列,第![]() 行的公差为
行的公差为![]() ,且每一列也是等差数列,设第
,且每一列也是等差数列,设第![]() 行的第
行的第![]() 项为
项为![]() .
.
(1)证明:![]() 成等差数列,并用
成等差数列,并用![]() 表示
表示![]() (
(![]() );
);
(2)当![]() 时,将数列
时,将数列![]() 分组如下:(
分组如下:(![]() ),(
),(![]() ),(
),(![]() ),…(每组数的个数构成等差数列). 设前
),…(每组数的个数构成等差数列). 设前![]() 组中所有数之和为
组中所有数之和为![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,设![]() 是不超过20的正整数,当
是不超过20的正整数,当![]() 时,求使得不等式
时,求使得不等式![]() 恒成立的所有
恒成立的所有![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
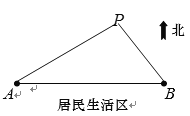
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com