
【题目】如图数表:

每一行都是首项为1的等差数列,第![]() 行的公差为
行的公差为![]() ,且每一列也是等差数列,设第
,且每一列也是等差数列,设第![]() 行的第
行的第![]() 项为
项为![]() .
.
(1)证明:![]() 成等差数列,并用
成等差数列,并用![]() 表示
表示![]() (
(![]() );
);
(2)当![]() 时,将数列
时,将数列![]() 分组如下:(
分组如下:(![]() ),(
),(![]() ),(
),(![]() ),…(每组数的个数构成等差数列). 设前
),…(每组数的个数构成等差数列). 设前![]() 组中所有数之和为
组中所有数之和为![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,设![]() 是不超过20的正整数,当
是不超过20的正整数,当![]() 时,求使得不等式
时,求使得不等式![]() 恒成立的所有
恒成立的所有![]() 的值.
的值.
【答案】(1)见解析,![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据前三行成等差数列得![]() ,根据最后一列成等差数列可得
,根据最后一列成等差数列可得![]() ,把
,把![]() 在第
在第![]() 行和第
行和第![]() 列分别表示出来,可得出
列分别表示出来,可得出![]() 关于
关于![]() 的表达式;
的表达式;
(2)根据分组的特点结合等差数列前![]() 和公式计算
和公式计算![]() ,利用错位相减法计算
,利用错位相减法计算![]() ;
;
(3)把![]() 代入不等式,得
代入不等式,得![]() ,引入函数
,引入函数![]() ,由函数的单调性可求得使不等式成立的
,由函数的单调性可求得使不等式成立的![]() 的最小值即可得
的最小值即可得![]() 的取值.
的取值.
解:(1) 由题意![]() ,
,![]() ,
,![]() 且
且![]() ,
,
得![]() ,即
,即![]()
所以![]() 成等差数列
成等差数列
由![]() 且
且![]()
即![]()
![]()
![]()
化简得![]()
(2) 当![]() 时,
时,![]()
按数列![]() 分组规律,第
分组规律,第![]() 组中有
组中有![]() 个奇数,
个奇数,
所以第1组到第![]() 组共有
组共有![]() 个奇数.
个奇数.
则前![]() 个奇数的和为
个奇数的和为![]() ,
,
即![]() ,
,![]()
从而 ![]()
![]() ,
,
![]() ,①则
,①则
![]() ,②
,②
①-②得![]() ,
,
∴![]() .
.
(3) 由![]() 得
得![]() .
.
令![]() ,
,
当![]() 时,都有
时,都有![]() ,即
,即![]() ,
,
而![]() ,
,
且当![]() 时,
时,![]()
![]() ,即
,即![]() 单调递增,故有
单调递增,故有![]() .
.
所以,满足条件的所有正整数![]() .
.


科目:高中数学 来源: 题型:
【题目】如果一个四面体的三个面是直角三角形,下列三角形:(1)直角三角形;(2)锐角三角形;(3)钝角三角形;(4)等腰三角形;(5)等腰直角三角形.那么可能成为这个四面体的第四个面是_____.(填上你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{2n﹣1}的前n项1,3,7,…,2n﹣1组成集合![]() (n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
(n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是
的定义域是![]() ,且
,且![]() ,
,![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)求![]() 在区间
在区间![]() 上的解析式;
上的解析式;
(3)是否存在整数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 有解?证明你的结论.
有解?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
科目:高中数学 来源: 题型:
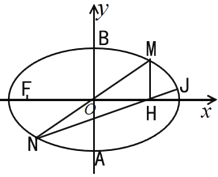
【题目】已知椭圆![]() 的左焦点为F,短轴的两个端点分别为A、B,且
的左焦点为F,短轴的两个端点分别为A、B,且![]() ,
,![]() 为等边三角形.
为等边三角形.
(1)求椭圆C的方程;
(2)如图,点M在椭圆C上且位于第一象限内,它关于坐标原点O的对称点为N;过点M作x轴的垂线,垂足为H,直线![]() 与椭圆C交于另一点J,若
与椭圆C交于另一点J,若![]() ,试求以线段
,试求以线段![]() 为直径的圆的方程;
为直径的圆的方程;
(3)已知![]() 是过点A的两条互相垂直的直线,直线
是过点A的两条互相垂直的直线,直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 与椭圆C交于另一点R;求
与椭圆C交于另一点R;求![]() 面积取最大值时,直线
面积取最大值时,直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,若椭圆的左、右焦点分别为
,若椭圆的左、右焦点分别为![]() ,
,![]() ,椭圆上一动点
,椭圆上一动点![]() 和
和![]() ,
,![]() 组成
组成![]() 的面积最大为
的面积最大为![]() .
.
(1)求椭圆的方程;
(2)若存在直线![]() :
:![]() 和椭圆相交于不同的两点
和椭圆相交于不同的两点![]() ,
,![]() ,且原点
,且原点![]() 与
与![]() ,
,![]() 连线的斜率之和满足:
连线的斜率之和满足:![]() .求直线
.求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com