
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,若椭圆的左、右焦点分别为
,若椭圆的左、右焦点分别为![]() ,
,![]() ,椭圆上一动点
,椭圆上一动点![]() 和
和![]() ,
,![]() 组成
组成![]() 的面积最大为
的面积最大为![]() .
.
(1)求椭圆的方程;
(2)若存在直线![]() :
:![]() 和椭圆相交于不同的两点
和椭圆相交于不同的两点![]() ,
,![]() ,且原点
,且原点![]() 与
与![]() ,
,![]() 连线的斜率之和满足:
连线的斜率之和满足:![]() .求直线
.求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】如图数表:

每一行都是首项为1的等差数列,第![]() 行的公差为
行的公差为![]() ,且每一列也是等差数列,设第
,且每一列也是等差数列,设第![]() 行的第
行的第![]() 项为
项为![]() .
.
(1)证明:![]() 成等差数列,并用
成等差数列,并用![]() 表示
表示![]() (
(![]() );
);
(2)当![]() 时,将数列
时,将数列![]() 分组如下:(
分组如下:(![]() ),(
),(![]() ),(
),(![]() ),…(每组数的个数构成等差数列). 设前
),…(每组数的个数构成等差数列). 设前![]() 组中所有数之和为
组中所有数之和为![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,设![]() 是不超过20的正整数,当
是不超过20的正整数,当![]() 时,求使得不等式
时,求使得不等式![]() 恒成立的所有
恒成立的所有![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,![]() (
(![]() 为圆柱的高,为球的半径,
为圆柱的高,为球的半径,![]() ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为![]() 千元,半球形部分每平方米建造费用为
千元,半球形部分每平方米建造费用为![]() 千元.设该储油罐的建造费用为
千元.设该储油罐的建造费用为![]() 千元.
千元.
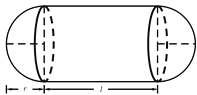
(1) 写出![]() 关于
关于![]() 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2) 若预算为![]() 万元,求所能建造的储油罐中
万元,求所能建造的储油罐中![]() 的最大值(精确到
的最大值(精确到![]() ),并求此时储油罐的体积
),并求此时储油罐的体积![]() (单位: 立方米,精确到
(单位: 立方米,精确到![]() 立方米).
立方米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() :
:![]() 的距离之比为
的距离之比为![]() ,求证:动点
,求证:动点![]() 的轨迹是椭圆;
的轨迹是椭圆;
(2)设(1)中的椭圆短轴的上顶点为![]() ,试找出一个以点
,试找出一个以点![]() 为直角顶点的等腰直角三角形
为直角顶点的等腰直角三角形![]() ,并使得
,并使得![]() 、
、![]() 两点也在椭圆上,并求出
两点也在椭圆上,并求出![]() 的面积;
的面积;
(3)对于椭圆![]() (常数
(常数![]() ),设椭圆短轴的上顶点为
),设椭圆短轴的上顶点为![]() ,试问:以点
,试问:以点![]() 为直角顶点,且
为直角顶点,且![]() 、
、![]() 两点也在椭圆上的等腰直角三角形
两点也在椭圆上的等腰直角三角形![]() 有几个?
有几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,∠PAD=90°,CD∥AB,∠BAD=90°,且AB=3CD=3PA![]() AD=3.
AD=3.
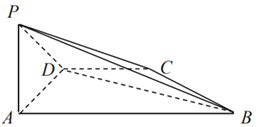
(1)求证:BD⊥PC;
(2)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是两条不同直线,
是两条不同直线,![]() ,
,![]() 是两个不同平面,给出下列四个命题:
是两个不同平面,给出下列四个命题:
①若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行;
平行;
②若![]() ,
,![]() 平行于同一平面,则
平行于同一平面,则![]() 与
与![]() 平行;
平行;
③若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线;
平行的直线;
④若![]() ,
,![]() 不平行,则
不平行,则![]() 与
与![]() 不可能垂直于同一平面
不可能垂直于同一平面
其中真命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com