
【题目】已知三棱锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,设点
,设点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上一点,且
上一点,且![]() .
.
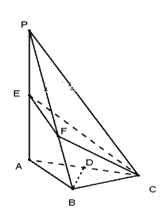
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】
已知函数![]() 为自然对数的底数)
为自然对数的底数)
(1)求![]() 的单调区间,若
的单调区间,若![]() 有最值,请求出最值;
有最值,请求出最值;
(2)是否存在正常数![]() ,使
,使![]() 的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出
的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出![]() 的值,以及公共点坐标和公切线方程;若不存在,请说明理由.
的值,以及公共点坐标和公切线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
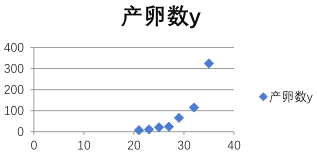
【题目】只红铃虫的产卵数y和温度x有关,现收集了7组观测数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
27 | 81 | 3.6 | 152 | 2936 | 38 |
其中![]()
(1)根据散点图判断,![]() 与
与![]() (e为自然对数的底数
(e为自然对数的底数![]() )哪一个更适宜作为红铃虫的产卵数y和温度x的回归方程类型?(给出判断即可,不必说明理由)
)哪一个更适宜作为红铃虫的产卵数y和温度x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)根据(2)的结果,当温度为37度时红铃虫的产卵数y的预报值是多少?
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其线性回归方程
,其线性回归方程![]() 的系数的最小二乘法估计值为
的系数的最小二乘法估计值为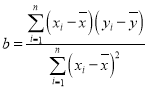 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为![]() ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
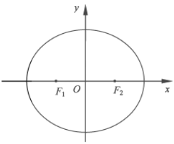
(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
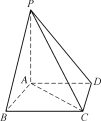
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求
①顾客所获的奖励额为60元的概率
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点P(2,1),且离心率为
经过点P(2,1),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设O为坐标原点,在椭圆短轴上有两点M,N满足![]() ,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长均相等的四棱锥![]() 中,
中, ![]() 为底面正方形的中心,
为底面正方形的中心, ![]() ,
,![]() 分别为侧棱
分别为侧棱![]() ,
,![]() 的中点,有下列结论正确的有:( )
的中点,有下列结论正确的有:( )

A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com