
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)若函数![]() 在区间
在区间![]() 上存在唯一零点,求a的取值范围.
上存在唯一零点,求a的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)分别在![]() 和
和![]() 两种情况下根据导函数的正负得到
两种情况下根据导函数的正负得到![]() 单调性,根据极值的定义可求得对应的极值;
单调性,根据极值的定义可求得对应的极值;
(2)当![]() 时,分别在
时,分别在![]() 上存在唯一零点和
上存在唯一零点和![]() 为零点两种情况下,结合零点存在定理得到
为零点两种情况下,结合零点存在定理得到![]() 的范围;当
的范围;当![]() 时,结合函数的单调性,可知
时,结合函数的单调性,可知![]() ,通过讨论
,通过讨论![]() 的位置确定对应端点值的符号,从而得到不等式组,解不等式组求得结果;综合两种情况可得最终结果.
的位置确定对应端点值的符号,从而得到不等式组,解不等式组求得结果;综合两种情况可得最终结果.
(1)由题意得:![]() .
.
①当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() 无极值;
无极值;
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 处取得极小值,极小值为
处取得极小值,极小值为![]() ,无极大值.
,无极大值.
综上所述:当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,无极值;
,无单调递减区间,无极值;
当![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,极小值为
,极小值为![]() ,无极大值.
,无极大值.
(2)①当![]() 时,由(1)知,
时,由(1)知,![]() 在
在![]() 上单调递增,
上单调递增,
若![]() 在
在![]() 上存在唯一零点,则
上存在唯一零点,则![]() ,即
,即![]() ,
,
解得:![]() .
.
若![]() 是
是![]() 在
在![]() 上的唯一零点,则
上的唯一零点,则![]() ,解得:
,解得:![]() (舍).
(舍).
②当![]() 时,由(1)知,
时,由(1)知,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() .
.
![]() ,
,
![]() 若
若![]() 在
在![]() 上存在唯一零点,则
上存在唯一零点,则![]() 或
或 或
或 ,
,
解得:![]() .
.
综上所述:![]() 的取值范围为
的取值范围为![]() .
.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】我省某校要进行一次月考,一般考生必须考5门学科,其中语、数、英、综合这四科是必考科目,另外一门在物理、化学、政治、历史、生物、地理、英语2中选择.为节省时间,决定每天上午考两门,下午考一门学科,三天半考完.
(1)若语、数、英、综合四门学科安排在上午第一场考试,则“考试日程安排表”有多少种不同的安排方法;
(2)如果各科考试顺序不受限制;求数学、化学在同一天考的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当![]() 时,
时,![]() (
(![]() ).
).
(1)当![]() 时,求
时,求![]() 的表达式:
的表达式:
(2)求![]() 在区间
在区间![]() 的最大值
的最大值![]() 的表达式;
的表达式;
(3)当![]() 时,若关于x的方程
时,若关于x的方程![]() (a,
(a,![]() )恰有10个不同实数解,求a的取值范围.
)恰有10个不同实数解,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交大设计学院植物园准备用一块边长为4百米的等边ΔABC田地(如图)建立芳香植物生长区、植物精油提炼处与植物精油体验点.田地内拟建笔直小路MN、AP,其中M、N分别为AC、BC的中点,点P在CN上.规划在小路MN和AP的交点O(O与M、N不重合)处设立植物精油体验点,图中阴影部分为植物精油提炼处,空白部分为芳香植物生长区,A、N为出入口(小路宽度不计).为节约资金,小路MO段与OP段建便道,供芳香植物培育之用,费用忽略不计,为车辆安全出入,小路AO段的建造费用为每百米4万元,小路ON段的建造费用为每百米3万元.
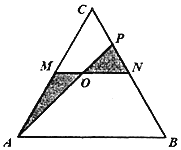
(1)若拟建的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(2)设∠BAP=![]() ,求
,求![]() 的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com