
【题目】甲、乙两支球队进行总决赛,比赛采用五场三胜制,即若有一队先胜三场,则此队为总冠军,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为二分之一.据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
(1)求总决赛中获得门票总收入恰好为150万元且甲获得总冠军的概率;
(2)设总决赛中获得的门票总收入为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】已知m、n∈R+ , f(x)=|x+m|+|2x﹣n|.
(1)求f(x)的最小值;
(2)若f(x)的最小值为2,证明:4(m2+ ![]() )的最小值为8.
)的最小值为8.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意(x1 , y1)∈M,存在(x2 , y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={ ![]() };
};
②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};
④M={(x,y)|y=ex﹣2}.
其中是“垂直对点集”的序号是( )
A.①②
B.②③
C.①④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,为一台冷轧机的示意图,冷轧机由若干对轧辊组成,带钢从一端输入,经过各对轧辊逐步减薄后输出.(轧钢过程中,钢带宽度不变,且不考虑损耗)
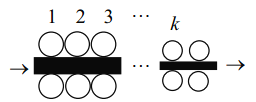
一对对轧辊的减薄率![]() .
.
(1)输入钢带的厚度为![]() ,输出钢带的厚度为
,输出钢带的厚度为![]() ,若每对轧辊的减薄率不超过
,若每对轧辊的减薄率不超过![]() ,问冷轧机至少需要安装几对轧辊?
,问冷轧机至少需要安装几对轧辊?
(2)已知一台冷轧机共有4对减薄率为![]() 的轧辊,所有轧辊周长均为
的轧辊,所有轧辊周长均为![]() ,若第
,若第![]() 对轧辊有缺陷,每滚动一周在刚带上压出一个疵点,在冷轧机输出的刚带上,疵点的间距为
对轧辊有缺陷,每滚动一周在刚带上压出一个疵点,在冷轧机输出的刚带上,疵点的间距为![]() ,易知
,易知![]() ,为了便于检修,请计算
,为了便于检修,请计算![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a2=3,a5=81,bn=1+2log3an .
(1)求数列{bn}的前n项的和;
(2)已知数列 ![]() 的前项的和为Sn , 证明:
的前项的和为Sn , 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E.
(Ⅰ)证明:∠ADE=∠AED;
(Ⅱ)若AC=AP,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com