
已知函数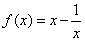 ,
,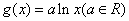 .
.
(1)a≥-2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为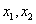 ,其中
,其中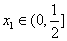 ,求
,求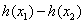 的最小值.
的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定。空气质量指数越高,代表空气污染越严重:
| 空气质量指数 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | ≥250 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
经过对某市空气质量指数进行一个月(30天)监测,获得数据后得到条形图统计图如图:
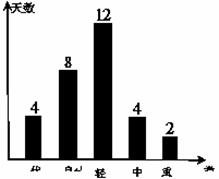
(1)估计某市一个月内空气受到污染的概率(规定:空气质量指数大于或等于75,空气受到污染);
(2)在空气质量类别为“良”、“轻度污染”、 “中度污染”的监测数据中用分层抽样方法抽取一个容量为6的样本,若在这6数据中任取2个数据,求这2个数据所对应的空气质量类别不都是轻度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图1,在直角梯形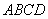 中,
中, ,
,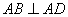 ,且
,且 .
.
现以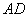 为一边向梯形外作正方形
为一边向梯形外作正方形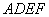 ,然后沿边
,然后沿边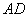 将正方形
将正方形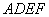 翻折,使平面
翻折,使平面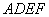 与平面
与平面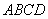 垂直,
垂直,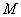 为
为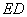 的中点,如图2.
的中点,如图2.
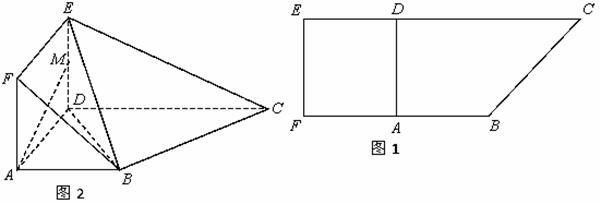
(1)求证: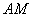 ∥平面
∥平面 ;
;
(2)求证: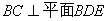 ;
;
(3)求点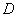 到平面
到平面 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
设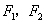 分别是椭圆
分别是椭圆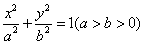 的左、右焦点,
的左、右焦点,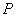 为椭圆上的任意一点,满足
为椭圆上的任意一点,满足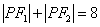 ,
,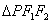 的周长为12.
的周长为12.
(1)求椭圆的方程;
(2)求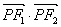 的最大值和最小值;
的最大值和最小值;
(3)已知点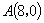 ,
, ,是否存在过点
,是否存在过点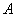 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点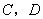 ,使得
,使得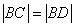 ?若存在,求直线
?若存在,求直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com