
分析 (1)根据对数不等式的解法即可求集合M;
(2)求出集合N,结合集合关系N⊆M,建立不等式关系即可得到结论.
解答 解:(1)M={x|log${\;}_{\frac{1}{2}}$($\frac{x}{2}$-1)≥0}=M={x|0<$\frac{x}{2}$-1≤1}={x|2<x≤4}.
(2)由(x-3)(2a+1-x)>0得(x-3)[x-(2a+1)]<0,
若2a+1=3得a=1,此时不等式不成立,
若2a+1>3,即a>1,则不等式的解为3<x<2a+1,即N=(3,2a+1),
若2a+1<3,即a<1,则不等式的解为2a+1<x<3,即N=(2a+1,3),
若N⊆M,
当a>1时,满足2a+1≤4,即1<a≤$\frac{3}{2}$,
若a<1时,满足2a+1≥2,即$\frac{1}{2}$≤a<1,
综上$\frac{1}{2}$≤a<1或1<a≤$\frac{3}{2}$.
点评 本题主要考查集合的基本运算,求出集合的等价条件是解决本题的关键.


科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(文)试卷(解析版) 题型:解答题
选修4—1:几何证明选讲.
如图,直线 过圆心
过圆心 ,交圆
,交圆 于
于 ,直线
,直线 交圆
交圆 于
于 (不与
(不与 重合),直线
重合),直线 与圆
与圆 相切于
相切于 ,交
,交 于
于 ,且与
,且与 垂直,垂足为
垂直,垂足为 ,连接
,连接 .
.

求证:(1) ;
;
(2) .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(文)试卷(解析版) 题型:解答题
在三角形 中,角
中,角 的对边分别为
的对边分别为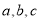 ,且三角形的面积为
,且三角形的面积为 .
.
(1)求角 的大小;
的大小;
(2)已知 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
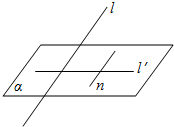 如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:
如图,设直线l是平面α的一条射线,l′是l在α内的射影,直线n?α.用<a,b>表示直线a,b的夹角.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com