
分析 (1)设出圆心的坐标,利用半径相等求得t,进而利用两点的距离公式求得半径,则圆的方程可得.
(2)线段CD中点M(x,y),C(x1,y1),由题意知x1=2x-4,y1=2y-3,由点A在圆(x+1)2+y2=4上运动,能求出点M的轨迹方程.
解答 解:(1)设圆心的坐标为(t,t+1),
则有(t-1)2+(t+1)2=(t+1)2+(t+3)2,
整理求得t=-1,
故圆心为(-1,0),r2=(t-1)2+(t+1)2=4,
则圆的方程为(x+1)2+y2=4.
(2)设线段CD中点M(x,y),C(x1,y1),
由题意知:x1=2x-4,y1=2y-3,
∵点C在圆(x+1)2+y2=4上运动,
∴(2x-4+1)2+(2y-3)2=4,
∴M的轨迹方程为(x-1.5)2+(y-1.5)2=1.
点评 本题考查线段的中点的轨迹方程的求法,考查代入法的运用,确定坐标之间的关系是关键.


科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:选择题
几何体的俯视图为一边长为2的正三角形,则该几何体的各个面中,面积最大的面的面积为( )
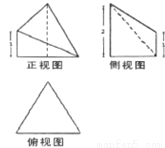
A.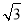 B.2 C.
B.2 C.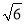 D.3
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
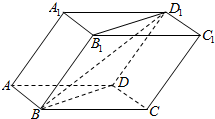 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{\sqrt{39}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{21}}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $13\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+x | B. | -x2+x | C. | -x2-x | D. | x2-x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com