
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:选择题
2015年11月11日的“双十一”又掀购物狂潮,淘宝网站对购物情况做了一项调查,收回的有效问卷共500000份,其中购买下列四种商品的人数统计如下:服饰鞋帽198000人;家居用品94000人;化妆品116000人;家用电器92000人.为了解消费者对商品的满意度,淘宝网站用分层抽样的方法从中选出部分问卷进行调查,已知在购买“化妆品”这一类中抽取了116人,则在购买“家居用品”这一类中应抽取的问卷份数为( )
A.92 B.94 C.116 D.118
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
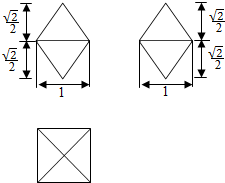
| A. | $\frac{{\sqrt{2}}}{3}π$? | B. | $\sqrt{2}π$? | C. | 2π? | D. | $\frac{{2\sqrt{2}}}{3}π$? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
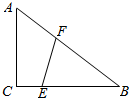 如图,在△ABC中,∠C=90°,AC=3,BC=4,AB边(包括端点)上一点F,BC边(包括端点)上一点E满足线段EF分△ABC的面积为相等的两部分;
如图,在△ABC中,∠C=90°,AC=3,BC=4,AB边(包括端点)上一点F,BC边(包括端点)上一点E满足线段EF分△ABC的面积为相等的两部分;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com