
分析 (1)将f(x)化简成y=Asin(ωx+φ)形式,带入周期公式求出;
(2)利用正弦定理将条件化简得出C,根据f($\frac{B}{2}$)取最大值求出B,然后解三角形.
解答 解:(1)f(x)=$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$=$\overrightarrow{a}$2+$\overrightarrow{a}•\overrightarrow{b}$=1+sinxcosx+$\sqrt{3}$cos2x=1+$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x+$\frac{\sqrt{3}}{2}$=sin(2x+$\frac{π}{3}$)+1+$\frac{\sqrt{3}}{2}$.
∴f(x)的最小正周期T=$\frac{2π}{2}$=π.
(2)∵acosB+bcosA=2ccosC,∴sinAcosB+sinBcosA=2sinCcosC,即sin(A+B)=2sinCcosC.
∴cosC=$\frac{1}{2}$.∴C=$\frac{π}{3}$.
f($\frac{B}{2}$)=sin(B+$\frac{π}{3}$)+1+$\frac{\sqrt{3}}{2}$.∵0<B<$\frac{2π}{3}$,∴当B+$\frac{π}{3}$=$\frac{π}{2}$,即B=$\frac{π}{6}$时,f($\frac{B}{2}$)取得最大值,
∴A=$\frac{π}{2}$.∴b=c•tanB=1,∴S△ABC=$\frac{1}{2}bc$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了三角函数的恒等变换与求值,正弦定理在解三角形中的应用,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:解答题
设函数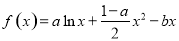 ,
,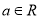 且
且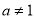 .曲线
.曲线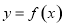 在点
在点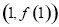 处的切线的斜率为
处的切线的斜率为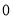 .
.
(1)求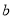 的值;
的值;
(2)若存在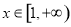 ,使得
,使得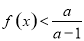 ,求
,求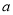 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${({\frac{4}{3}})^{n-1}}$ | B. | ${({\frac{3}{4}})^{n-1}}$ | C. | 3n-1 | D. | ${({\frac{1}{3}})^{n-1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com