
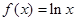 ,
, 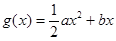
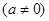 .
.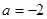 , 函数
, 函数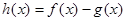 在其定义域是增函数,求
在其定义域是增函数,求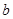 的取值范围;
的取值范围;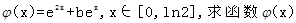 的最小值;
的最小值;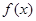 的图象
的图象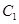 与函数
与函数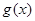 的图象
的图象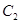 交于点
交于点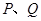 ,过线段
,过线段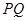 的中点
的中点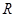 作
作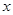 轴的垂线分别交
轴的垂线分别交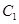 、
、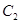 于点
于点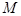 、
、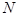 ,问是否存在点
,问是否存在点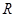 ,使
,使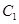 在
在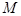 处的切线与
处的切线与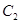 在
在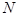 处的切线平行?若存在,求出
处的切线平行?若存在,求出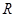 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.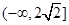 ;(2)当
;(2)当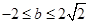 时,
时,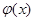 的最小值为
的最小值为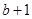 ;当
;当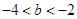 时,
时,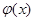 的最小值为
的最小值为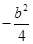 ;当
;当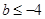 时,
时,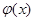 的最小值为
的最小值为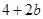 ;(3)不存在点.
;(3)不存在点.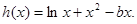
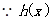 在
在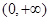 上是增函数,
上是增函数,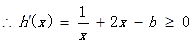 对
对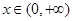 恒成立, 2分
恒成立, 2分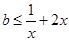
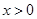 ,则
,则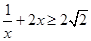 .
.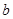 的取值范围为
的取值范围为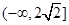 4分
4分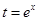 ,则函数化为
,则函数化为
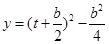
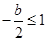 ,即
,即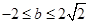 时,函数
时,函数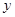 在
在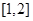 上为增函数.
上为增函数.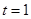 时,
时,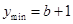 ; 6分
; 6分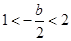 ,即
,即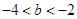 时,当
时,当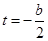 时,
时,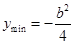 ;
;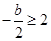 ,即
,即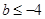 时,函数
时,函数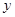 在
在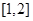 上是减函数.
上是减函数.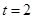 时,
时,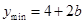 8分
8分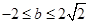 时,
时,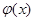 的最小值为
的最小值为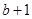 .
.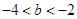 时,
时,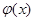 的最小值为
的最小值为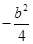 .
.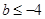 时,
时,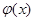 的最小值为
的最小值为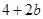 . 9分
. 9分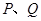 的坐标是
的坐标是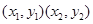 且
且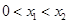 则点
则点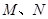 的横坐标为
的横坐标为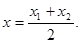
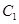 在点
在点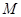 处的切线斜率为
处的切线斜率为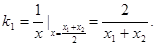
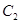 在点
在点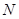 处的切线斜率为
处的切线斜率为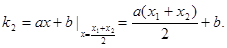 10分
10分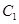 在点
在点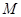 处的切线与
处的切线与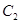 在点
在点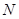 处的切线平行,则
处的切线平行,则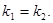
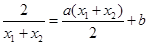 11分
11分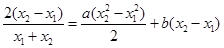
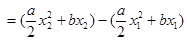
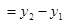
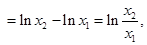
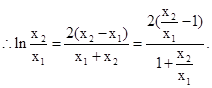
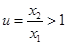 ,则
,则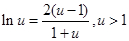 ① 12分
① 12分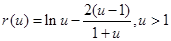 ,则
,则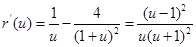
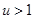 ,∴
,∴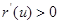 ,所以
,所以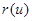 在
在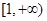 上单调递增,
上单调递增,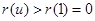 ,则
,则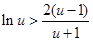 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
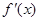 >
>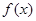 成立,则称函数
成立,则称函数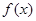 是D上的J函数.
是D上的J函数.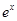 lnx是J函数时,求m的取值范围;
lnx是J函数时,求m的取值范围;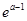 g(1)的大小;
g(1)的大小;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
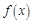 是偶函数,且当
是偶函数,且当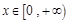 时,f (x) = x-1,则f (x-1) < 0的解集是( )
时,f (x) = x-1,则f (x-1) < 0的解集是( )| A.{x |-1 < x < 0} | B.{x | x < 0或1< x < 2} |
| C.{x | 0 < x < 2} | D.{x | 1 < x < 2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com