
分析 (Ⅰ)当直线l的斜率为1,解方程组$\left\{{\begin{array}{l}{y=x-1}\\{{y^2}=4x}\end{array}}\right.$,消去y得x2-6x+1=0,由韦达定理得x1+x2=6,即可求线段MN的长;
(Ⅱ)记t=$\frac{1}{|FM|}+\frac{1}{|FN|}$,分类讨论,利用韦达定理求t的值.
解答 解:(Ⅰ)由题意知,抛物线的焦点F(1,0),准线方程为:x=-1.…(1分)
设M(x1,y1),N(x2,y2),由抛物线的定义知|MF|=x1+1,|NF|=x2+1,
于是|MN|=|MF|+|NF|=x1+x2+2.…(3分)
由F(1,0),所以直线l的方程为y=x-1,
解方程组$\left\{{\begin{array}{l}{y=x-1}\\{{y^2}=4x}\end{array}}\right.$,消去y得x2-6x+1=0.…(4分)
由韦达定理得x1+x2=6,
于是|MN|=x1+x2+2=8
所以,线段MN的长是8.…(6分)
(Ⅱ)设M(x1,y1),N(x2,y2),
当直线l的斜率不存在时,M(1,2),N(1,-2),$t=\frac{1}{|FM|}+\frac{1}{|FN|}=1$;…(7分)
当直线l的斜率不存在时,设直线l方程为y=k(x-1)
联立$\left\{{\begin{array}{l}{y=k(x-1)}\\{{y^2}=4x}\end{array}}\right.$消去x得k2x2-(2k2+4)x+k2=0,△=16k2+16>0,
${x_1}+{x_2}=\frac{{2{k^2}+4}}{k^2}=2+\frac{4}{k^2}$,x1x2=1…(9分)
$t=\frac{1}{|FM|}+\frac{1}{|FN|}=\frac{1}{{{x_1}+1}}+\frac{1}{{{x_2}+1}}=\frac{{{x_1}+{x_2}+2}}{{{x_1}{x_2}+{x_1}+{x_2}+1}}$=$\frac{{\frac{4}{k^2}+4}}{{1+\frac{4}{k^2}+2+1}}=1$…(11分)
所以,所求t的值为1. …(12分)
点评 本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查分类讨论的数学思想,属于中档题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
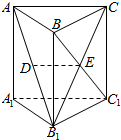 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证:
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
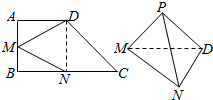 在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.
在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com