
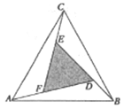
【题目】赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽炫图”(以弦为边长得到的正方形组成).类比“赵爽弦图”,可类似地构造如下图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设![]() ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是__________.
,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是__________.
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在![]() 轴上的抛物线
轴上的抛物线![]() 过点
过点![]() ,椭圆
,椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,其中
,其中![]() 与
与![]() 的焦点重合,过
的焦点重合,过![]() 与长轴垂直的直线交椭圆
与长轴垂直的直线交椭圆![]() 于
于![]() 两点且
两点且![]() ,曲线
,曲线![]() 是以原点为圆心以
是以原点为圆心以![]() 为半径的圆.
为半径的圆.
(1)求![]() 与
与![]() 及
及![]() 的方程;
的方程;
(2)若动直线![]() 与圆
与圆![]() 相切,且与
相切,且与![]() 交与
交与![]() 两点,三角形
两点,三角形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将4个编号为1、2、3、4的小球放人编号为1、2、3、4的盒子中.
(1)恰好有一个空盒,有多少种放法?
(2)每个盒子放一个球,且恰好有一个球的编号与盒子的编号相同,有多少种放法?
(3)把4个不同的小球换成4个相同的小球,恰有一个空盒,有多少种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
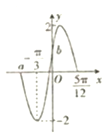
【题目】函数f(x)=Asin(2ωx+φ)(A>0,ω>0,|φ|<![]() )的部分图象如图所示
)的部分图象如图所示
(1)求A,ω,φ的值;
(2)求图中a,b的值及函数f(x)的递增区间;
(3)若α∈[0,π],且f(α)=![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)![]() (x∈R),有下述四个结论:
(x∈R),有下述四个结论:
①任意x∈R,等式f(﹣x)+f(x)=0恒成立;
②任意x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2);
③存在m∈(0,1),使得方程|f(x)|=m有两个不等实数根;
④存在k∈(1,+∞),使得函数g(x)=f(x)﹣kx在R上有三个零点.
其中包含了所有正确结论编号的选项为( )
A.①②③④B.①②③C.①②④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年,“非典”爆发,以钟南山为代表的医护工作者经长期努力,抗击了非典.
年,“非典”爆发,以钟南山为代表的医护工作者经长期努力,抗击了非典.![]() 年
年![]() 岁高龄的钟院士再次披挂上阵,逆行武汉抗击新冠疫情。为调查中学生对这一伟大“逆行者”的了解程度,某调查小组随机抽取了某市物化生、政史地的
岁高龄的钟院士再次披挂上阵,逆行武汉抗击新冠疫情。为调查中学生对这一伟大“逆行者”的了解程度,某调查小组随机抽取了某市物化生、政史地的![]() 名高中生,请他们列举钟南山院士在医学上的成就,把能列举钟南山成就不少于
名高中生,请他们列举钟南山院士在医学上的成就,把能列举钟南山成就不少于![]() 项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:
项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:
组合 | 0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 |
物化生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
政史地(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)请将下面的2×2列联表补充完整;
组合 | 比较了解 | 不太了解 | 合计 |
物化生 | |||
政史地 | |||
合计 |
(2)判断是否有99%的把握认为,了解钟南山与选择物化生、政史地组合有关?
参考:![]()
![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com