
【题目】已知焦点在![]() 轴上的抛物线
轴上的抛物线![]() 过点
过点![]() ,椭圆
,椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,其中
,其中![]() 与
与![]() 的焦点重合,过
的焦点重合,过![]() 与长轴垂直的直线交椭圆
与长轴垂直的直线交椭圆![]() 于
于![]() 两点且
两点且![]() ,曲线
,曲线![]() 是以原点为圆心以
是以原点为圆心以![]() 为半径的圆.
为半径的圆.
(1)求![]() 与
与![]() 及
及![]() 的方程;
的方程;
(2)若动直线![]() 与圆
与圆![]() 相切,且与
相切,且与![]() 交与
交与![]() 两点,三角形
两点,三角形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]()
![]()
![]() ; (2)
; (2)![]() .
.
【解析】
(1)先利用点的坐标求抛物线的方程,再根据题意分别求出椭圆和圆的方程;
(2)设出直线方程,求出面积的表达式,根据表达式的特点,求出范围.
(1)由已知设抛物线方程为![]() 则
则![]() ,解得
,解得![]() ,
,
即![]() 的方程为
的方程为![]() ;焦点坐标为
;焦点坐标为![]() ,
,
所以椭圆中![]() ,其焦点也在
,其焦点也在![]() 轴上设方程为
轴上设方程为![]()
由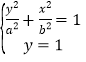 得
得![]() ,
, ![]() 又
又![]() 解得
解得![]()
椭圆方程为![]() ,
,
又![]() 所以所求圆的方程为
所以所求圆的方程为![]() ,
,
(2) 因为直线![]() 与圆
与圆![]() 相切,所以圆心O到直线的距离为1,
相切,所以圆心O到直线的距离为1,
所以![]() ,
,
当直线![]() 的斜率不存在时方程为
的斜率不存在时方程为![]() ,两种情况所得到的三角形
,两种情况所得到的三角形![]() 面积相等,
面积相等,
由 得
得![]() ,不妨设
,不妨设![]() ,
, ![]()
此时 ![]() ,
,
当直线![]() 的斜率存在时设为
的斜率存在时设为![]() ,直线方程为
,直线方程为![]()
所以圆心O到直线的距离为![]() 即
即![]() ,
,
由 得
得![]()
所以![]()
![]()
![]() 恒大于0,
恒大于0,
设![]() 则
则![]()
所以![]()
![]()
![]()
![]() ,
,
令![]() 则
则![]() ,
,![]()
所以![]()
![]() 是关于
是关于![]() 的二次函数开口向下,在
的二次函数开口向下,在![]() 时单调递减,
时单调递减,
所以![]() ,综上:
,综上: ![]() .
.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】毕业季有![]() 位好友欲合影留念,现排成一排,如果:
位好友欲合影留念,现排成一排,如果:
(1)![]() 、
、![]() 两人不排在一起,有几种排法?
两人不排在一起,有几种排法?
(2)![]() 、
、![]() 两人必须排在一起,有几种排法?
两人必须排在一起,有几种排法?
(3)![]() 不在排头,
不在排头,![]() 不在排尾,有几种排法?
不在排尾,有几种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一段长度为![]() 的木棍,希望将其锯成尽可能多的小段,要求每一小段的长度都是整数,并且任何一个时刻,当前最长的一段都严格小于当前最短的一段长度的2倍,记对
的木棍,希望将其锯成尽可能多的小段,要求每一小段的长度都是整数,并且任何一个时刻,当前最长的一段都严格小于当前最短的一段长度的2倍,记对![]() 符合条件时的最多小段数为
符合条件时的最多小段数为![]() ,则( )。
,则( )。
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.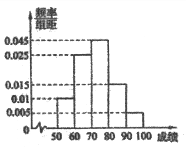
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽炫图”(以弦为边长得到的正方形组成).类比“赵爽弦图”,可类似地构造如下图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设![]() ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是__________.
,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是__________.
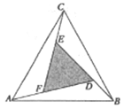
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面ABCD.
平面ABCD.
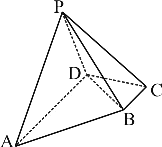
(1)求证:![]() ;
;
(2)在线段PA上是否存在一点M,使二面角M-BC-D的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com