(1)解:设方程2x
2+4x-30=0的两个实根为α,β,
则α+β=-2,αβ=-15,
∵函数f(x)=x
2+ax+b(a,b为实常数)的零点与函数g(x)=2x
2+4x-30的零点相同,
∴x
2+ax+b=0的两个实根为α,β,
由韦达定理得a=-(α+β)=2,b=αβ=-15.
(2)证明:由(1)知f(x)=x
2+2x-15,
从而2a
n+1=a
n(a
n+2),即

,
∵2a
n+1=a
n(a
n+2),
∴
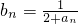
=

=

=

,
∴T
n=b
1•b
2•b
3…b
n=
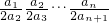
=
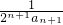
.
S
n=b
1+b
2+…+b
n=(

)+(
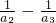
)+…+(

)
=

,n∈N
*.
∴对任意正整数n,2
n+1T
n+S
n=

+

=2为定值.
(3)证明:∵a
1>0,
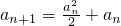
,
∴a
n+1>a
n>0,n∈N
*即{a
n}为单调递增的正数数列,
∵

,
∴{b
n}为递减的正数数列,且
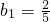
,
∴

,
∵

,
∴对任意正整数n,都有2[1-(

)
n]≤S
n<2.
分析:(1)设方程2x
2+4x-30=0的两个实根为α,β,则α+β=-2,αβ=-15,由函数f(x)=x
2+ax+b(a,b为实常数)的零点与函数g(x)=2x
2+4x-30的零点相同,知x
2+ax+b=0的两个实根为α,β.由韦达定理能求出a和b.
(2)证明:由(1)知f(x)=x
2+2x-15,从而

,所以

=

,由此能够证明对任意正整数n,2
n+1T
n+S
n=

+

为定值.
(3)由a
1>0,
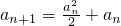
,知{a
n}为单调递增的正数数列,由

,知{b
n}为递减的正数数列,由此能够证明对任意正整数n,都有2[1-(

)
n]≤S
n<2.
点评:本题考查数列与不等的综合应用,综合性强,强度大,计算繁琐,容易出错.解题时要认真审题,注意韦达定理的合理运用,注意培养计算能力.

 ,2an+1=f(an)+15,bn=
,2an+1=f(an)+15,bn=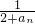 (n∈N*).
(n∈N*). )n]≤Sn<2.
)n]≤Sn<2. ,
,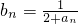 =
=
 =
= ,
,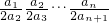
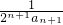 .
. )+(
)+(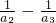 )+…+(
)+…+( )
) ,n∈N*.
,n∈N*. +
+ =2为定值.
=2为定值.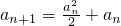 ,
, ,
,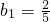 ,
, ,
, ,
, )n]≤Sn<2.
)n]≤Sn<2. ,所以
,所以 =
= ,由此能够证明对任意正整数n,2n+1Tn+Sn=
,由此能够证明对任意正整数n,2n+1Tn+Sn= +
+ 为定值.
为定值.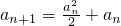 ,知{an}为单调递增的正数数列,由
,知{an}为单调递增的正数数列,由 ,知{bn}为递减的正数数列,由此能够证明对任意正整数n,都有2[1-(
,知{bn}为递减的正数数列,由此能够证明对任意正整数n,都有2[1-( )n]≤Sn<2.
)n]≤Sn<2.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<