
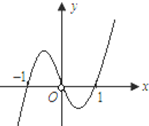
 已知函数y=
已知函数y=| f′(x) |
| x |
| A、f′(1)=f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf′(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |
| f′(x) |
| x |
| f′(x) |
| x |
| f′(x) |
| x |
| f′(x) |
| x |
| f′(x) |
| x |


科目:高中数学 来源: 题型:
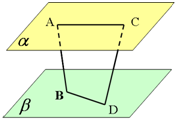 已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.
已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:
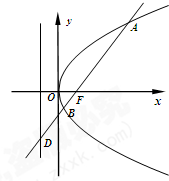 如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.
如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:
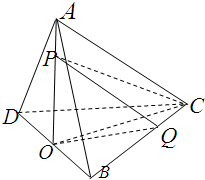 如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为
如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
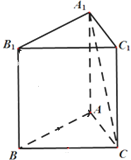 在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证:
在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证:查看答案和解析>>
科目:高中数学 来源: 题型:
| A、在统计里,从总体中抽取的一部分个体叫做总体的一个样本,样本中个体的数目叫做样本的容量 |
| B、一组数据的平均数一定大于这组数据中的每个数据 |
| C、平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 |
| D、一组数据的方差越大,说明这组数据的波动性越大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com