
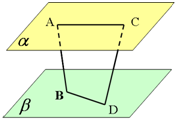
 已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.
已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.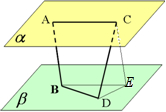 解、过C作CE∥AB交β于E,连接BE、DE,
解、过C作CE∥AB交β于E,连接BE、DE,

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
| 18 |
| 5 |
A、cosA=
| ||
B、cosA=-
| ||
C、cosB=
| ||
D、cosB=-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{1,2,3} |
| B、{1,3,9} |
| C、{1,5,7} |
| D、{3,5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
| C、a+3 | ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
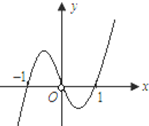 已知函数y=
已知函数y=| f′(x) |
| x |
| A、f′(1)=f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf′(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 1+an |
| 1 |
| 1-an+1 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com