
分析 解分式不等式$\frac{x-1}{x+1}≥0$即可得出集合A={x|x<-1,或x≥1},根据a<1便可判断B≠∅,从而根据B⊆A便可建立关于a的不等式组,解不等式组即可得出实数a的取值范围.
解答 解:解$\frac{x-1}{x+1}≥0$得,x<-1,或x≥1;
∴A={x|x<-1,或x≥1};
∵a<1;
∴2a-(a+1)=a-1<0;
∴2a<a+1;
∴B≠∅;
∵B⊆A;
∴$\left\{\begin{array}{l}{2a≥1}\\{a<1}\end{array}\right.$,或$\left\{\begin{array}{l}{a+1<-1}\\{a<1}\end{array}\right.$;
解得$\frac{1}{2}≤a<1$,或a<-2;
∴实数a的取值范围为$(-∞,-2)∪[\frac{1}{2},1)$.
故答案为:(-∞,-2)∪[$\frac{1}{2}$,1).
点评 考查描述法表示集合的定义及表示形式,分式不等式的解法,子集的定义.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
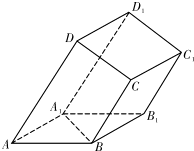 如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1.
如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:填空题
在一次连环交通事故中,只有一个人需要负主要责任,但在警察询问时,甲说:“主要责任在乙”;乙说:“丙应负主要责任”;丙说“甲说的对”;丁说:“反正我没有责任”.四人中只有一个人说的是真话,则该事故中需要负主要责任的人是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com