
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{7}{2}$ |
分析 由向量数量积的坐标运算公式得$\overrightarrow{OM}$•$\overrightarrow{ON}$=2x+y,作出题中不等式组表示的平面区域得到如图的阴影部分,
将目标函数z=2x+y对应的直线进行平移,当x=y=$\frac{1}{2}$时z=2x+y取得最小值,即为所求.
解答 解:∵M(2,1),N(x,y),∴目标函数z=$\overrightarrow{OM}$•$\overrightarrow{ON}$=2x+y;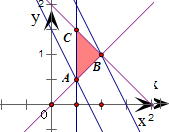
作出不等式组$\left\{\begin{array}{l}{x+y≤2}\\{x≥\frac{1}{2}}\\{y≥x}\end{array}\right.$表示的平面区域,
得到如图所示的△ABC及其内部,
其中A($\frac{1}{2}$,$\frac{1}{2}$),B(1,1),C($\frac{1}{2}$,$\frac{3}{2}$)
设z=F(x,y)=2x+y,将直线l:z=2x+y进行平移,
当l经过点A时,目标函数z取得最小值;
∴z最小值=F($\frac{1}{2}$,$\frac{1}{2}$)=2×$\frac{1}{2}$+$\frac{1}{2}$=$\frac{3}{2}$.
故选:C.
点评 本题考查了二元一次不等式组表示平面区域、向量数量积的坐标运算公式和简单的线性规划等知识,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
中秋节吃月饼是我国的传统习俗,设一盘中盛有7块月饼,其中五仁月饼2块,莲蓉月饼3块,豆沙月饼2块,这三种月饼的形状大小完全相同,从中任取3块.
(Ⅰ)求这三种月饼各取到1块的概率;
(Ⅱ)设 表示取到的豆沙月饼的个数,求
表示取到的豆沙月饼的个数,求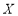 的分布列,数学期望与方差.
的分布列,数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com