
分析 (1)根据函数奇偶性的定义判断函数f(x)=x|x-a|的奇偶性;
(2)分类讨论,即可求出在区间[0,1]上的最大值.
解答 解:(1)当a=0时,f(x)=-x|x|,则f(-x)=-x|x|=-f(x),
所以f(x)为奇函数.
当a≠0时,f(1)=|1-2a|,f(-1)=-|1+2a|,
∵|1-2a|+|1+2a|≠0,
∴f(-1)≠f(1),
故f(x)不是偶函数;
又a≠0时,∵|1-2a|≠|1+2a|,
∴f(-1)≠-f(1),
故f(x)不是奇函数,
总之,当a≠0时,函数f(x)是非奇非偶函数.
综上,当a=0时,f(x)为奇函数;当a≠0时,函数f(x)是非奇非偶函数.
(2)x∈[0,1]时,f(x)=x|x-2a|=|x2-2ax|=|(x-a)2-a2|.
记h(x)=x2-2ax=(x-a)2-a2.
①当a≤0时,h(x)在区间[0,1]上为增函数,且h(x)≥0.
因此a≤0时,g(a)=h(1)=1-2a,
②当a≥1时,h(x)在区间[0,1]上为减函数,且h(x)≤0.
因此a≥1时,g(a)=-h(1)=2a-1,
③当0<a<1时,h(x)在区间[0,a]上为减函数,在[a,1]上为增函数.
因为h(0)=0,h(a)=-a2,h(1)=1-2a,g(a)是|h(a)|=a2与|h(1)|=|1-2a|中较大者.
由(a2)2-(1-2a)2=(a2-2a+1)(a2+2a-1)=(a-1)2(a2+2a-1),
以及0<a<1知:
当$0<a<\sqrt{2}-1$时,(a2)2-(1-2a)2<0,a2<|1-2a|=1-2a;
当$\sqrt{2}-1≤a<1$时,(a2)2-(1-2a)2≥0,a2>|1-2a|.
所以,当$0<a<\sqrt{2}-1$时,g(a)=1-2a;当$\sqrt{2}-1≤a<1$时,g(a)=a2.
综合①②③得,$g(a)=\left\{\begin{array}{l}1-2a{,^{\;}}a<\sqrt{2}-1\\{a^2},\sqrt{2}-1≤a<1\\ 2a-1{,^{\;}}a≥1\end{array}\right.$
点评 本题主要考查函数奇偶性的判断,以及分段函数的最值的求法,考查学生的运算能力.


科目:高中数学 来源: 题型:选择题
| A. | 2x+y-z=0 | B. | x+y-2z=0 | C. | x+y-z+3=0 | D. | 2x-y-z-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
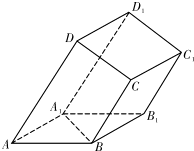 如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1.
如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:填空题
在一次连环交通事故中,只有一个人需要负主要责任,但在警察询问时,甲说:“主要责任在乙”;乙说:“丙应负主要责任”;丙说“甲说的对”;丁说:“反正我没有责任”.四人中只有一个人说的是真话,则该事故中需要负主要责任的人是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com